Dr. Neil Balmforth
RESEARCH INTERESTS
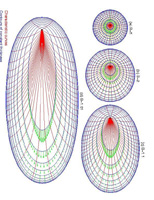
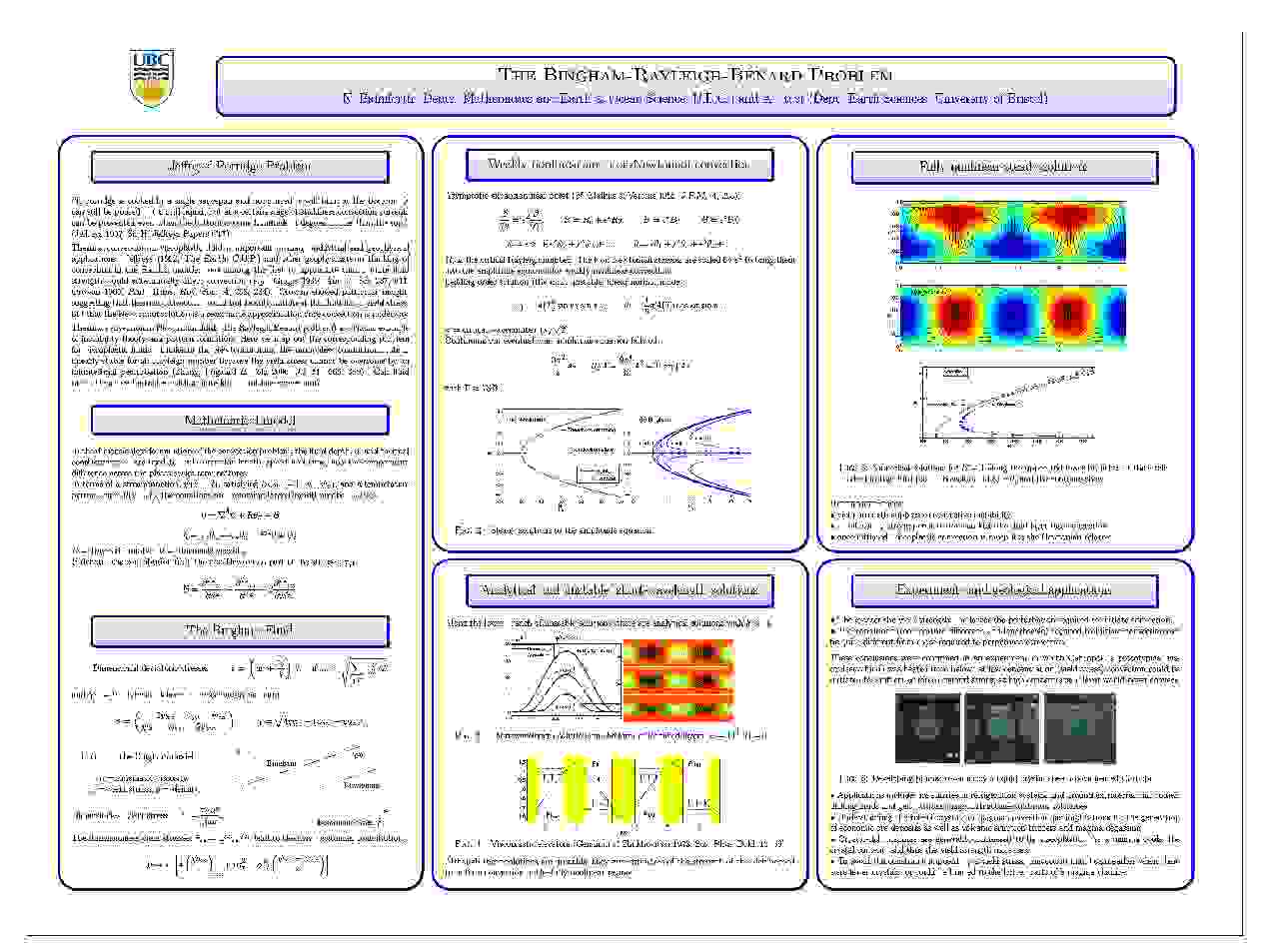
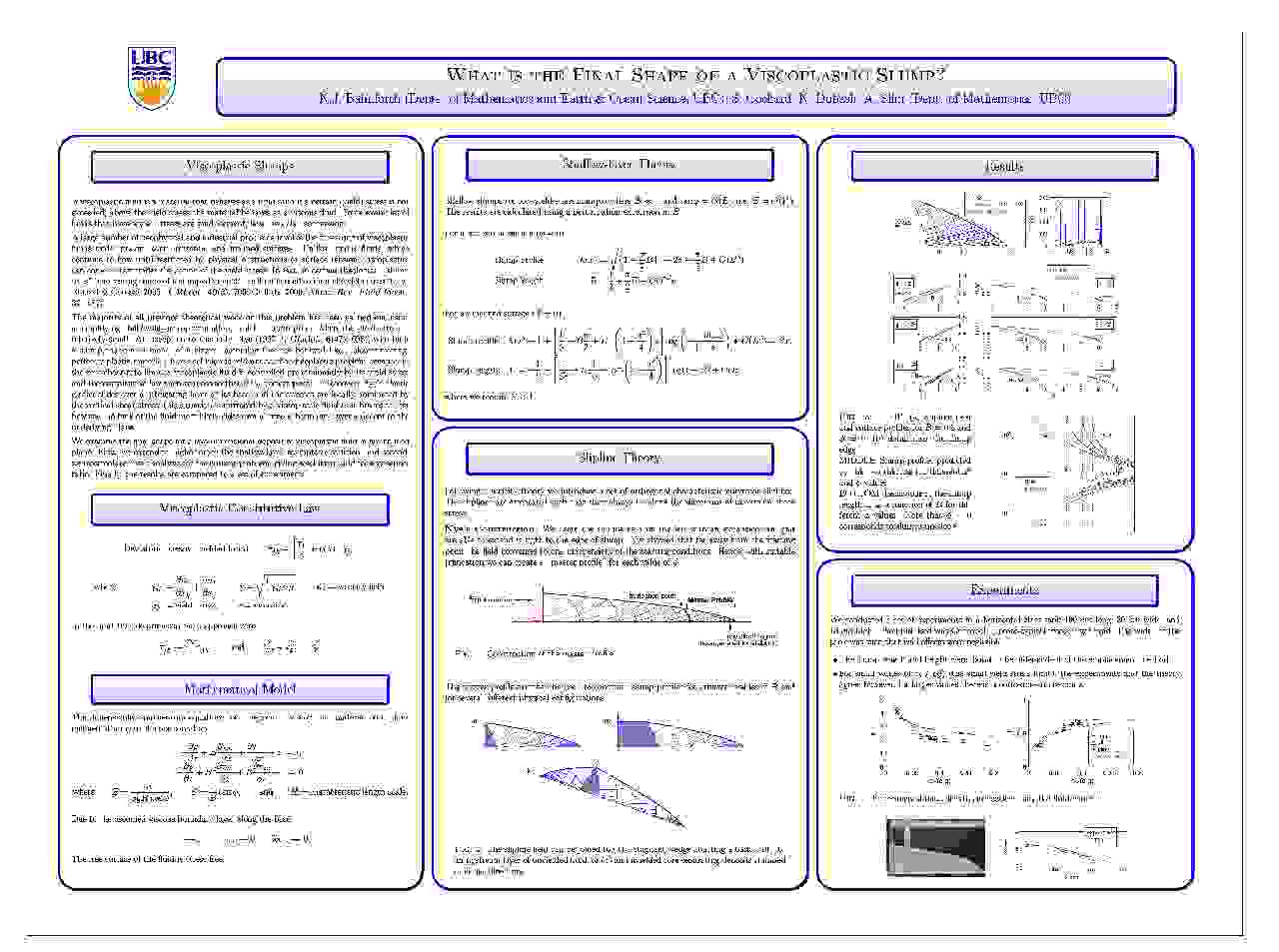
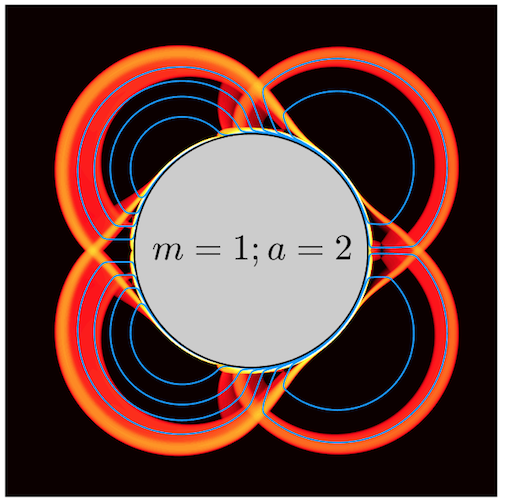
Non-Newtonian Fluid Dynamics And Applications In Geophysics:
Aside from air and water, most of the fluids we encounter in physical and industrial processes are "non-Newtonian" (meaning that there is no simple relationship between the stress and the rate of strain). Often, the 'rheology' arises because the fluid in question builds up a microstructure at the molecular level which becomes sufficiently extensive to affect the macroscopic properties of the fluid. In lava, for example, the microstructure is provided by a network of interlocked silicate crystals, and endows the fluid with an internal strength that allows lava to withstand a certain amount of imposed stress before it flows. Unfortunately, fluid models that build in the rheology significantly complicate the governing equations. My work in this area is focused on simplifying these equations to gain insight into the flow dynamics. For example, for lava flow, the main goal is to develop a "shallow-lava theory". That is, a general theoretical model that incorporates the essential physical ingredients and can be used to compute the flow of lava under terrestrial and extra-terrestrial conditions. Computations with the full three-dimensional equations is an inefficient route for such a model, partly because the rheology of cooling lava is so complicated. But by using asymptotic methods, simpler versions can be built for use by geologists. Related geological problems include mud flows and glacier mechanics. The rheology of mud and ice has several similarities with that of lava, and the same non-Newtonian fluid models can be used to describe how they flow. Similar models are also used for landslides, avalanches, and the dynamics of sand. These materials are mostly granular media, and require a different physical framework. However, the underlying idea (the reduction of governing equations to simpler, useful models) is a powerful tool that can be brought to bear in these applications also.
Much of my work is theoretical, focussing on mathematical modelling, but I also do experiments (some of which took place in the backyard and cellar; occasionally even in a lab).
I have many collaborators in these efforts, including Richard Craster and Richard Kerswell.
Much of my work is theoretical, focussing on mathematical modelling, but I also do experiments (some of which took place in the backyard and cellar; occasionally even in a lab).
I have many collaborators in these efforts, including Richard Craster and Richard Kerswell.
Click to enlarge
Experiment showing a clay slurry flowing over an inclined plane
Viscoplastic flow around a knife
A model of an expanding, inclined dome of viscoplastic fluid
Dambreaks - Bostwick Consistometer
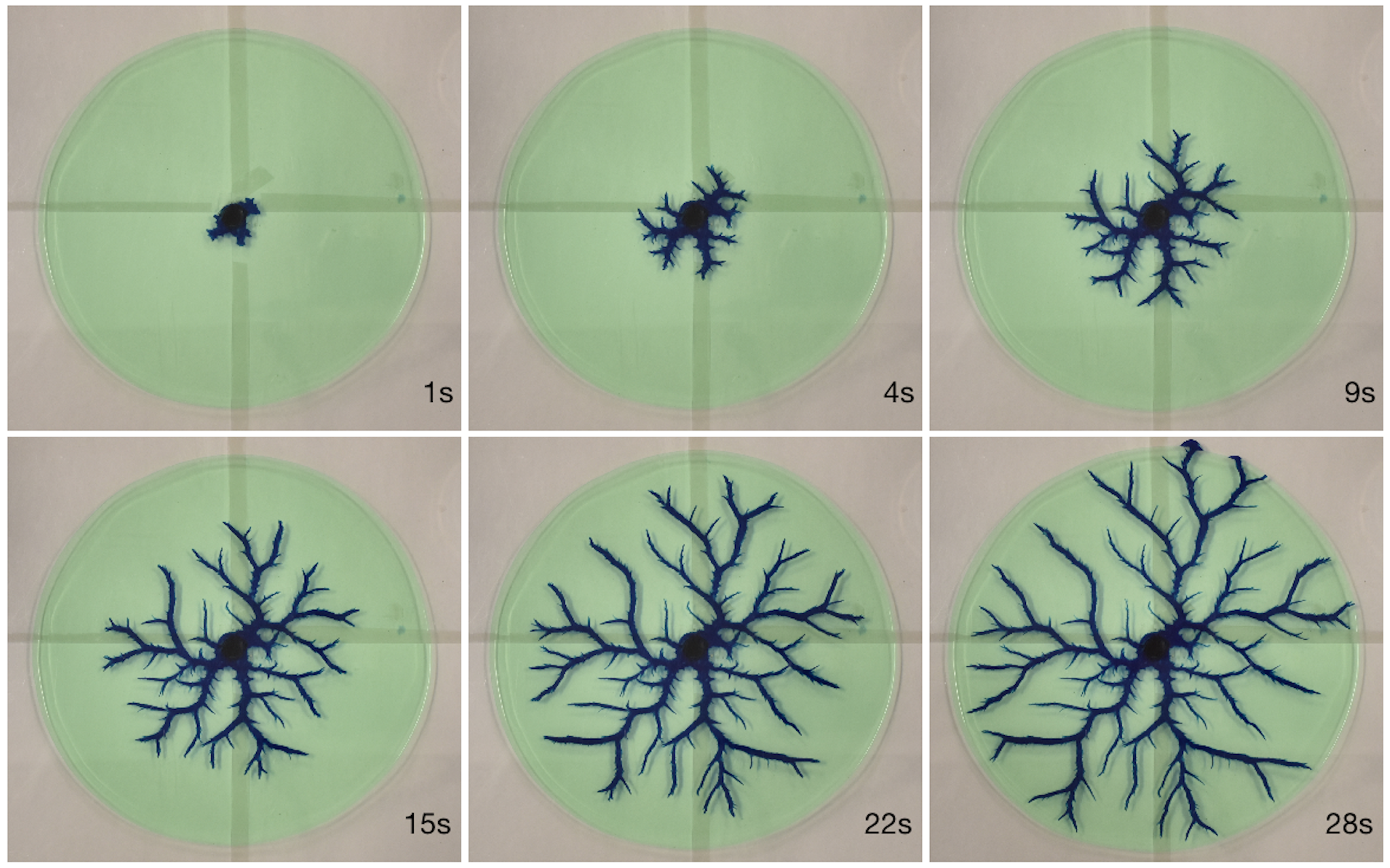
Fingering of a viscoplastic contact line
The viscoplastic Stokes layer
Viscoplastic drips I and II
Thixotropic gravity currents
Axisymmetric dambreaks
Viscoplastic Bretherton problem
Swimming in mud
Swimming in mud II
Translating and squirming cylinders
Viscoplastic fingers and fractures I
Viscoplastic fingers and fractures II
Capillary rise with a yield stres
Fingering of a viscoplastic contact line
The viscoplastic Stokes layer
Viscoplastic drips I and II
Thixotropic gravity currents
Axisymmetric dambreaks
Viscoplastic Bretherton problem
Swimming in mud
Swimming in mud II
Translating and squirming cylinders
Viscoplastic fingers and fractures I
Viscoplastic fingers and fractures II
Capillary rise with a yield stres
Viscoplastic fractures in a slot
Severing Saffman-Taylor fingers
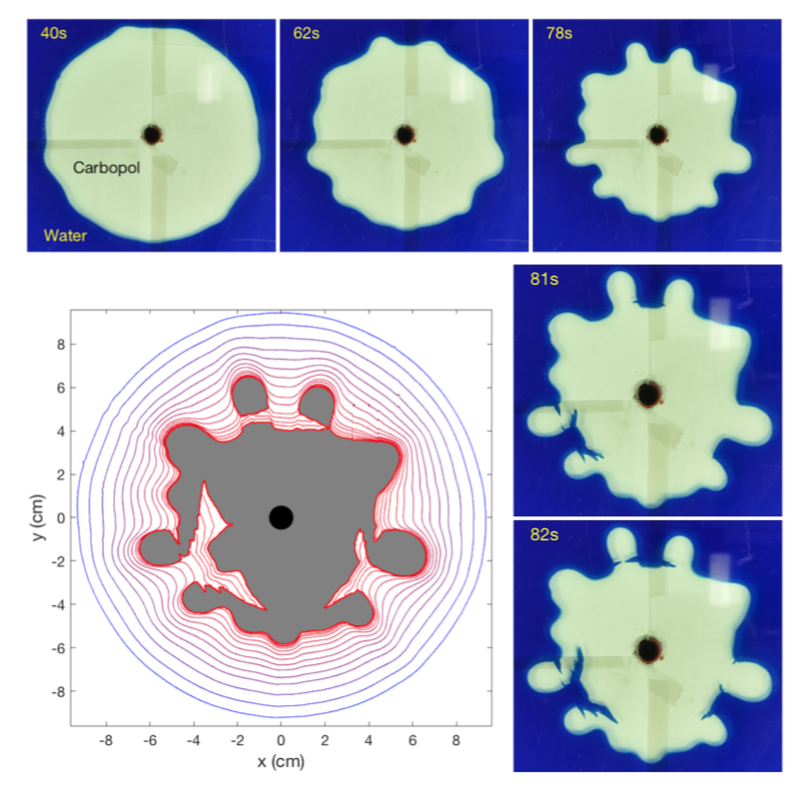
Carbi-flowers