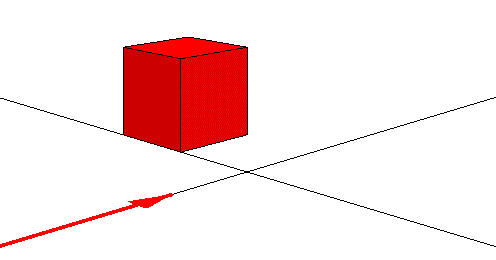
Consider an observer moving along the x axis towards the origin, as shown below.

What does the observer see as he moves towards it at non-relativistic speeds? Just as you would expect, a rectangle growing larger until he passes it. If, just as he passes the line y=0, he glances sideways, he will see the side of the building, another rectangle.
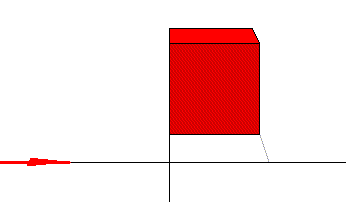
This is all boring so far. Now imagine that he can move at a significant fraction of the speed of light, and takes the same path at this speed towards the building.
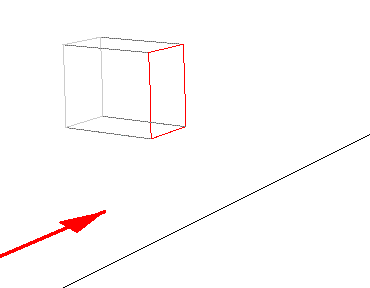
(The red face is the front.) This time, as he approaches the building, he is going to see something very different because the speed of light is no longer negligible. Lines perpendicular to his direction of motion are going to appear curved while lines parallel are going to be contracted. The whole building is also going to appear rotated, and his field of view is going to be compressed in the forwards direction, and expanded in the reverse direction; objects behind him will be rotated into sight. I will now explain each of these effects.
Continue with an explanation of Lorentz contraction
Continue directly to Terrell rotation
Continue directly to an explanation of the curvature