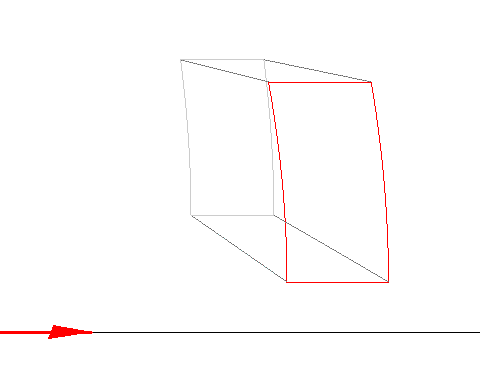

In the previous section, we assumed that the angular field of view was small. If that assumption is not made, how do the results change? As the picture above promises, lines perpendicular to the direction of motion appear curved into hyperbolas. Why?
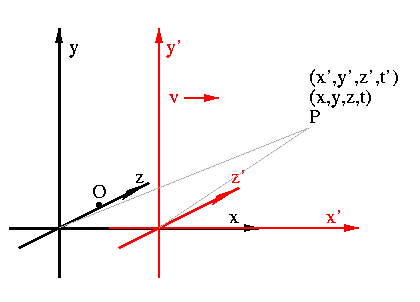
Consider the standard reference frames we have been using: place the observer at rest in a reference frame, K, with K' moving in the x direction, with velocity v, such that the x axes are incident and the origins coincide at t=t'=0. Place the observer at (0,0,d) in K. Now, for O', the origin of K' to appear at O (the origin of K), light from O' must be emitted at t=0, and the instant of observation must be t=d/c. Light from any other point P' = (x',y',z') in K' which appears at P = (x,y,z) in K must have been emitted at
This is obtained by simple trigonometry; see the above picture. The part in {} is the distance from (0,0,d) to P, so the expression is: the time that light left O (i.e. d/c) minus the time for light to travel from P to (0,0,d). It is minus, of course, because if the point is farther away, the light must have left earlier.
Plugging this into the Lorentz transformations that were derived earlier gives
solving this for x
We are interested in the lines perpendicular to the x' axis, so setting x' to a constant, x' + (v/c)Gd = const = A gives
Which has the form of a shifted and stretched hyperboloid, 1 = x^2 - y^2 - z^2 . Hence, lines perpendicular to the direction of motion, the x' axis, appear hyperbolic in shape.
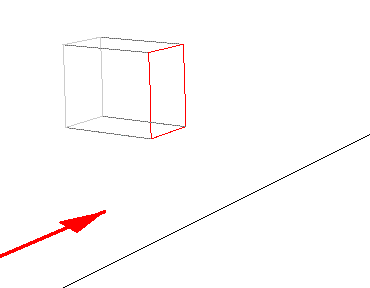
This is the image of a cube at 0.4c. The red face is the front.
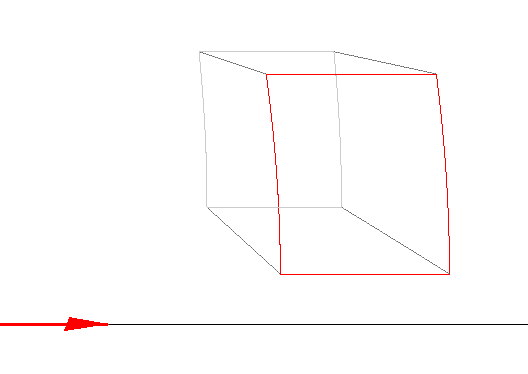
At 0.8c