To derive an expression for Lorentz Contraction, begin with the following postulates:

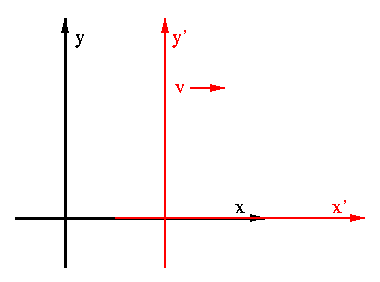
Consider two frames, one which will be assumed to be fixed, and another moving along a common x axis with a constant velocity relative to the first frame. This is shown above. We would like to be able to translate between coordinates in both frames. A coordinate, x', in the moving frame (K') is going to be dependent on x in the static frame (K), and also on the relative velocity, v, of the two frames, and the time that the even occurs in K.
where G is a constant, independent of the coordinates and time, and dependent on the relative velocity of the two frames.
Let the origins coincide at t=t'=0, and at this time, a flash of light is set off at the origin. An observer at P with coordinates (x,y,z,t) in K the rest frame, and (x',y',z',t') in K' observes the flash. As motion is only in the x=x' direction, the y and z coordinates are the same in both frames

And the x and x' coordinates must satisfy the following.
The Newtonian case would have t=t', but here we let the times in different frames be different.
Substituting these values into (*) and (**) above gives
Solving the bottom of these equations for t', and substituting into the top equation gives
The full transformations are then:
We have not started entirely from first principles, having guessed the initial forms of (*) and (**). This is the full derivation as it was given by Einstein. He begins by writing x' - ct' = M(x - ct) for some constant, M, independent of the coordinates, for propagation in the positive direction, and x + ct = L(x' + ct') for propagation in the negative direction. Adding and subtracting these equations yields almost (*) and (**), but with more constants to be determined. He then looks at a unit length measured in each coordinate system. By the above postulates, they must be equal and so the constants can be determined. The final result is of course what is given above.
And after all that, I will now show that, despite claims made by Einstein and Lorentz, this effect cannot actually be measured!
It would be nice if there were a more pictorial way to derive the Lorentz transformation, instead of relying on the algebra. The book Spinors and Space-time by Roger Penrose explains a way to consider Lorentz transformations as affine mappings of the Argand plane onto itself. Lorentz transformations can also be shown to be a subset of the group of quaternions, as is done by LJ Synge in Quaternions, Lorentz Transformations and the Conway-Dirac-Eddington Matrices. I have only briefly looked through these works, unfortunately having come across them too late to incorporate some of the results into this project.