In 1959, a paper by James Terrell appeared in the Physics Review Invisibility of the Lorentz Contraction. I will explain the effect that he realized.
We assume the following about the camera that is photographing the effect:
It was assumed for 50 years that the Lorentz contraction could be photographed; that objects would appear contracted in the direction of motion, and that that was the extent of the relativistic distortion. In 1959 James Terrell and Roger Penrose independently realized that this was not the case.

Consider the situation in the above picture; motion is in the positive x direction past the cube; the view is from above. What does the observer see if he glances at the cube just as he passes it. Because the speed of light is finite, the light he sees from the back corners, D and C, will have been transmitted earlier than light from the front corners, A and B. If the motion of the observer was not relativistic, but rather so slow that the speed of light could assumed to be infinite, then light from D would always run into the side of the cube, and so D would obviously only be seen (from positive x) when A, D and the observer were colinear.
However, if the motion is much faster, for the light from D and A to reach the observer at the same time, the light must have been emitted from D at an earlier time. Specifically, the light from D must travel a distance l greater than the light from A, so light from D must have been emitted when D had coordinate (x - lv/c, y, z)=D' as is shown below.
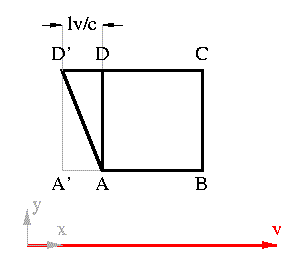
The light travels the distance l from D to A in dt=l/c. In this time, the cube has moved distance lv/c so that light from D can reach the observer (not be blocked by the cube). This light from D and newly emitted light from A then travel to the observer in the same time.
For the full effect, of course, the face containing A and B will be Lorentz contracted by a factor l/G. The corners D, A and B instead of having separation in the x direction of 0 and l will have separation lv/c and l/G. (Where G = (1 - (v/c)^2)^(-1/2), as before.)

This is exactly what would be observed if the whole cube was rotated by angle arcsin(v/c).
The cube, then appears to undergo a rotation when viewed at relativistic speeds. Note that there is no actual physical rotation, it is just an optical effect.