|
This is a short guide to a series of eleven papers in which a construction of an interacting Fermi liquid in two space dimensions is implemented. The main results are stated and proven in [FKTf1, FKTf2, FKTf3]. Theorem I.4 of [FKTf1] gives the convergence of the complete perturbation expansions of the temperature zero connected Green's functions for a system of weakly coupled Fermions with "asymmetric" Fermi surface. An outline of the proof is provided in §2 and § 3 of [FKTf1]. The complete proof - using the results of the auxiliary papers [FKTl], [FKTo1, FKTo2, FKTo3, FKTo4] and [FKTr1, FKTr2] - is given in [FKTf2]. The existence of a discontinuity in the particle number density at the Fermi surface is stated in Theorem I.5 of [FKTf1] and proven in [FKTf3]. Continuity properties of the amputated four point Green's functions, stated in Theorem I.7 of [FKTf1] are also proven in [FKTf3].
Our proof uses a multiscale analysis and discrete renormalization group
flow, in the framework of Fermionic functional integrals, and also uses
renormalization of the Fermi surface. We introduce a scale parameter
M>1 and in the jth step of the renormalization group flow
turn on interactions amongst particles whose momenta have
distance from the Fermi surface about
The treatment of the first renormalization group step, i.e. the ultraviolet regime, is a simple application of the expansion of [FKTr1] and appears in [FKTo2]. Control of the change of sectorization forced by the change of scales between renormalization group steps is achieved in [FKTo4].
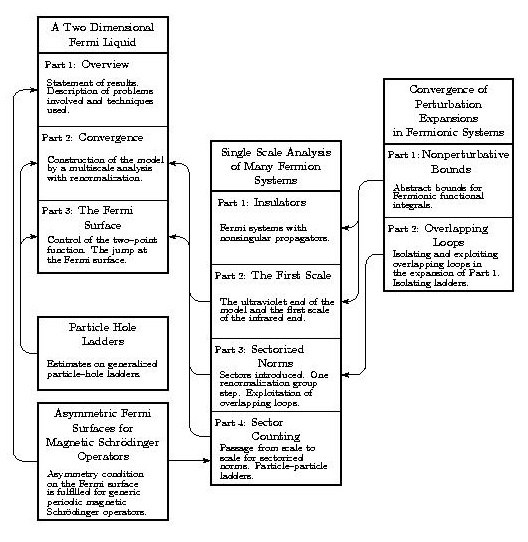
As mentioned above, [FKTf1] gives an overview of the construction. The paper [FKTo1], where nonsingular propagators (as is the case for insulators) are considered, can also serve as an introduction to some of the techniques. The set of eleven papers is self-contained. [FKTr1+FKTr2], [FKTl] and [FKTo4] are each reasonably independent of the other papers in the series. The interface between each of these and the other papers is through a relatively small number of Definitions and Theorems. The flow chart [pdf,jpg] below gives a thumbnail sketch of the contents of each of the papers and gives the logical connections between the papers.
