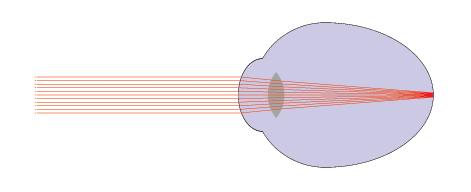
Lens
Corrections
It turns out glasses
correct our vision by "enhancing" the natural performance of our own
eyes. Even if an eye shows either near or far-sightedness, there is a
still a range in which that person can see clearly. The closest point at
which a person can see an object in perfect focus is called the "near
point". Similarly, there is a distance called a "far point" which
represents the farthest distance that a person can see a clear, focused
image. For a person with "perfect" vision, this range of clear vision is
around 25 cm for the near point, all the way out to "infinity". While an
eye cannot see all the way out to infinity, in terms of the size of our
eyes, anything over five meters represents infinity.
For someone who is
nearsighted, they are likely to have a near point that is even closer
than 25 cm. This is due to the fact that as an image moves closer to
one's eye, it focuses further and further back. The natural elongation
of the back of the eye in a near-sighted person allows it to focus even
when these objects are close. However, the far point for a near sighted
person is likely to be quite short; around 17 to 25 cm is average. For a
far sighted person, they can see off into "infinity", but can only focus
on objects that are a distance away from them (usually a meter or more
away).
The way that
lens helps us see is by adjusting light rays so that it gives the
"impression" that it came from that distance. At this point, it
would be handy to introduce some technical aspects.
Lens
Equation
This commonly used
formula is used to describe the relationship between three objects. An
object located dO units away from a lens with a focal length
f, will create an image with dI units away. They are related
as such:
1/(f)
= 1/(dO) + (1/dI)
where:
f is the focal length of the lens
dO is
the distance from the lens to the object
dI is
the distance from the lens to the object
There is a technical
term given the left hand side; 1/f , when f is measured in meters is
called the power of lens. The units have a special name called a diopter (D), and it is
defined as inverse meters or m-1. There is also a handed
convention when dealing with the two distance measurements. If an object
and its image are on the same side of a lens, then the image distance, dI,
is considered negative. If an object and its image are on opposite
sides of a lens, then both are considered positive. It turns out this
strange convention allows the lens equation to work under almost all
basic circumstances.
Let's take a
look at the near sighted case again:
In this case, the
lens that will be used is called a diverging
lens. What it is going to do is bend the rays so that light from
infinity "appears" as though it is coninciding with a person's far
point. In doing so, it allows the person to see a clear image, without
altering their depth perception. Here's a look at what the lens does:

The lens actually
bends the light outwards so that it looks like that it coming from a
source that is quite close. The following a quick sample calculation
that uses the lens equation.
EXAMPLE: Let's assume that there is a
near-sighted person which has a far point of 17 cm away from their eye.
How strong does the lens have to be so that the rays coming in from
"infinity" look like they are coming in from 17 cm? For this example,
let's say that the lens is about 2 cm away from the eye.
We know we would
like the object distance to be "infinity". We want the image to appear
17 cm in front of the person's eye; this happens to be 15 cm (=17 cm - 2
cm) in front of the lens. Since the object and image distance are on the
same side, we have to place a negative sign with the image distance, so
we use -15 cm instead of +15 cm. We can figure out the power of the lens:
1/f = -1/0.15 m + 1/∞
While it may not be
terribly obvious, we will treat 1/∞ as being
zero for this calculation. If one were to put in a real number, it would
only make a small contribution to the overall result. So we end up
getting:
1/f = -1/0.15 m + 0
1/f = -1/0.15 m = 6.667 m-1 =
6.667 D
As
such, we need to use a lens with a focal length of 0.15 meters, or a
power of 6.667 D. Now that we've let the person see images from far
away, can they still see images that are up close? Now that we have a
lens focal power, we can use information about the person's near point
to determine how it has moved.
EXAMPLE: Let's say that the same
person has a near point of 12 cm from their eye. With the lens on, how
far does an object 12 cm away appear to be?
As with before, the lens and the resultant image are still on the
same side, so we assign a negative sign for the image
distance. Since the near point is 12 cm with respect to the eye, it
happens to be 10 cm (= 12 cm - 2cm) away from the front of the lens. We
can plug in what we know into the lens equation.
1/(f)
= 1/(dO) + (1/dI)
1/(0.15
m) = 1/(0.10 m) - (1/dI)
1/(0.15
m) - 1/(0.10
m) = - (1/dI)
- (1/dI)
= 2/(0.30
m) - 3/(0.60
m)
(1/dI)
=0.30 m
The net result is
that the person sees the image as being about 30 cm away. This is fairly
close to how a person with "perfect" vision sees. What (a proper) lens
seems to do is take the furthest and nearest point at which we can see,
and adjusts it so that the world falls within the limitations of our
eye. Everything in the real world remains its proper distance; all that
happens is that the lens adjusts it so that the light enters our eye
that way.
Let's take a look at
far-sightedness now:
With a corrective lens, the following thing happens:
In this case, the
reverse happens from the near-sighted case. It takes all the rays coming
in from a source that is very close, and "straightens" them out so that
they look like they are coming in from infinity. The lens can be treated
in much the same way as the near sighted case.
EXAMPLE: For a particular far-sighted
person, they have a near point of 102 cm. How powerful does the lens
need to be if they person wants to see an object that 27 cm away from
their eye?
As with the first
case, the image and the actual object are on the same side, so the image
is considered negative. The real object is 25 cm (= 27cm - 2cm) away
from the front of the lens, and we want to produce an image that appears
to be 100 cm away (= 102 cm - 2 cm) from the lens. Plug everything into
the equation:
1/(f)
= 1/(dO) + (1/dI)
1/(f)
= 1/(0.25 m) - (1/1m)
1/(f)
= 4/(1 m) - (1/1m) = 3/(1m) = 3 m-1 =
3.00 D
The resulting lens
has a positive power, and is known as a converging lens. It "pulls in"
rays that are spreading out. Now that we have "fixed" this person's
vision at closer distances, what happens to objects at infinity? Since
all that the lens does is "straighten" out light, rays that are already
going in a straight line will only be effected slightly. This, in turn,
keeps the far point at infinity.
Astigmatism
There is one last
type of eye defect that we have not addressed. Astimagtism is an eye
defect in which people cannot properly on lines because their
corneas are out of shape. It turns out that people
with astimatism have corneas that are not spherical. As a result, light
that comes from a single point does not focus at a single point when it
goes through their eyes. It actually turns into a line.

In this image,
it the green lens is not a sphere; it is actually part of a
cylinder. This deviation from spherical shapes causes the light to
continue in a straight path when hitting a lens, instead of focusing
together. Unfortunately, there was insufficient time for me to fully
address this section, so I will have to leave it at that!
Introduction
Colour Vision
Colour Math
Approximations
Focal Lengths and
Distances
GRIN Systems
Human
Vision
Vision Problems
Corrections