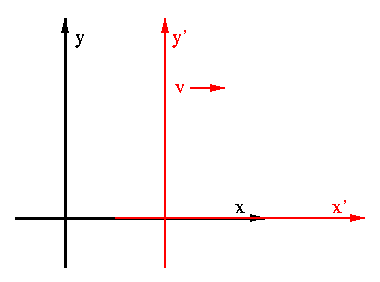
Derivation of Coordinate Transformations

To derive an expression for Lorentz Contraction, begin with the following postulates:

The laws of physics are the same in all inertial frames of reference
The speed has the same value, c, in all inertial frames

Consider two frames, one which will be assumed to be fixed, and another moving along a common x axis with a constant velocity relative to the first frame. This is shown above. A beam of light is propagating along the common x axis. In the first frame, this satisfies

x-ct = 0

and analogously in the second coordinate system

x'-ct'=0

That is, a constant of proportionality relates the equations in the two systems

(x'-ct') = L (x-ct)

(For the Newtonian case, this constant would be 1.)
Similarly, for light propagating along the negative x axis, except the constant may be different:

(x'-ct') = M (x-ct)

Adding and subtracting these equations, respectively gives

2x' = (L+M)x - (M-L)ct
2ct' = -(L-M)x + (L+M)ct

Defining new constants, a and b, these equations simplify to

x' = ax - ct
ct' = act - bx

So now, if we know a and b, we will be able to translate between one coordinate system and the other.

Continue