In this section, we will discuss three aspects of spherical mirrors:
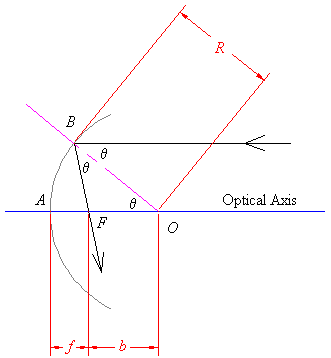
Consider a concave mirror as shown, with a light ray coming in parallel to the optical axis. The centre of the spherical mirror with radius R is located at O. The optical axis strikes the mirror at B and the ray in question hits the reflector at A.

From the Law of Reflection, and angle geometry of parallel lines, we know that the marked angles are equal. Hence we have an equilateral triangle AFO. We are interested in the location of point F; we want to know where rays from infinity get focussed. Dropping the median from F and using trigonometry, we can find the distances f and b.
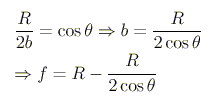
For small angles, the cosine is close to 1, so for rays close to the optical axis, the focus will be very nearly R/2, or halfway from the reflecting surface to the centre of curvature. For most of our work with mirrors, we will be using this approximation for the location of the focus. The distance from the surface to the focus is called the focal length, which we shall denote with the letter f.
From our diagram, we can see that the incident angle with the normal gets bigger as the ray deviates further from the optical axis. Cosine is a decreasing function for angles going from 0 to 90 degrees, so that the distance b takes up more of the space between the centre and surface of the mirror. Hence rays hitting the mirror further away from the axis of a concave spherical mirror are focussed closer to the mirror; this makes for a fuzzy image.
Concave parabolic mirrors have the happy property of focussing all rays from infinity to the exact same point. There is a truly remarkable proof of this; I regret that I do not have enough disk quota to include it1.
The location of the focus for a convex spherical mirror is also halfway between the centre and the surface, for rays close to the optical axis. The diagram is different; the proof falls out in the same way as for concave mirrors.
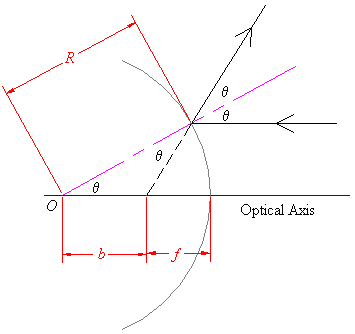
Notice that the focus of a convex mirror is not where the reflected rays converge; in fact the reflected rays do not converge at all. The reflected rays seem to diverge from the focus, for a convex mirror.
The image of an object in a concave mirror depends on the location of the object itself; we will deal with this presently.
Consider a concave mirror.
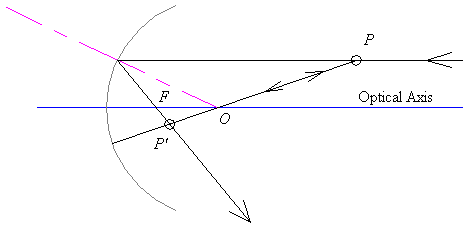
The point P of an object interacting with the mirror shall have an image P' whose location will be dictated by the Law of Reflection. All light rays from P should meet at P', so we can find the image point by finding the intersection of two reflected rays. In this case, it is easy to trace the rays that go through the centre of curvature (they reflect back on the same path, since they travel along the radii which are normal to the arc's surface), and the rays from infinity coming in parallel to the optical axis (they go through the focus, a distance R/2 away from the surface).
Measuring from the surface, when the source is beyond the centre of the mirror, we have the following picture.
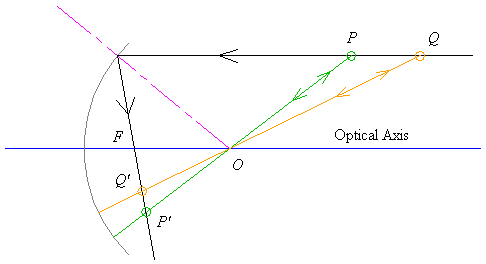
Tracing the mentioned rays, we see that the image of an object will be inverted; we also note that the image is shrunken (we shall deal the the magnitude of shrinkage in the next section). Since the image is not behind the mirror, the image can be caught on a screen (the image is real). Drawing a different point along the incident ray from infinity, we easily see that the image gets smaller as we move further away from the mirror's focus.
When the source is between the focus and the centre, we have the following picture.
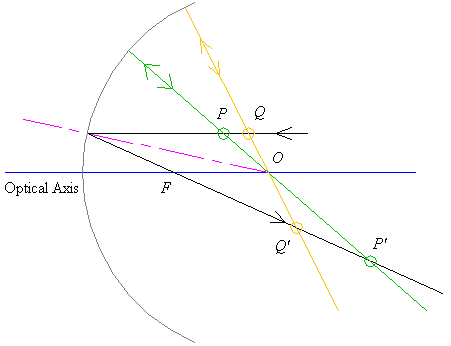
Tracing rays, we again see that the image will again be inverted and real. However, this time it is magnified. Note that as we move further from the focus, the image grows smaller, as in the previous case.
When the source is between the surface of the mirror and its focus, we have the following picture.
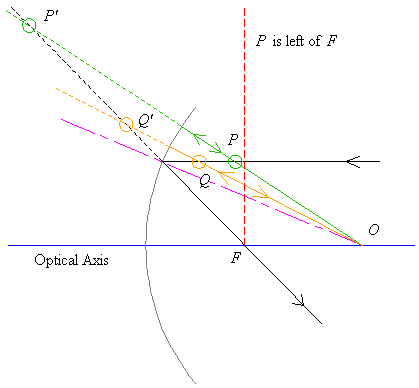
We see that the image is upright and magnified. The image is behind the mirror, so it is virtual, and cannot be caught on a screen. Again, as the source strays from the focus, the image grows smaller.
Dealing with convex mirrors is simpler here.
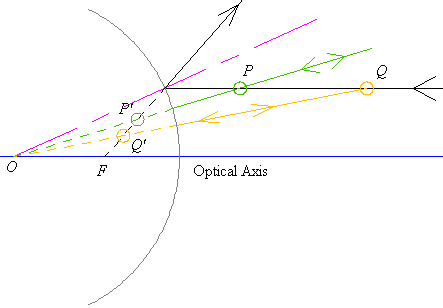
The object is necessarily on the side of the mirror opposite the focus F. As the diagram illustrates, the image is always upright, shrunken, and real. As we move away from the focus, the image grows smaller.
Before we take up our discussion of magnification, it will be useful to find the position of an image given the position of its originating object. Consider the following concave mirror, with an object beyond the centre of curvature. In what follows, we use radian measure for angles.
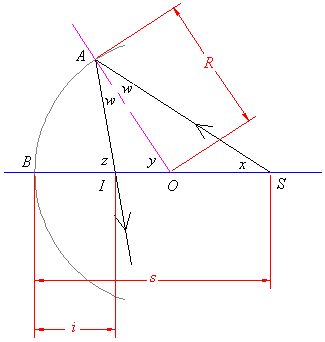
The object is placed at S, which is s units away from the surface of the mirror along the optical axis. The resulting image will be at I, which is i units away from the surface of the mirror. The mirror has radius R, and the angles w and x can be measured. Using the angle sum theorems for triangles and lines, we see that the angle y = w + x, or w = y - x. Similarly, z = y + w, or, substituting for w, we get z = 2y - x.
The arclength of AB is exactly AB = Ry. When we are dealing with small angles, the approximations AB = iz = sx hold. Isolating each of x, y, and z in these equations, and substituting into z = 2y - x, we see that
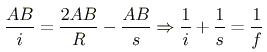
We have used the approximation f = R/2 for spherical mirrors.
In fact, this equation holds for all cases of spherical mirrors, regardless of the source's position, provided we use sign conventions for i, s, and f.
For a reflecting surface, let Side 1 be the side from which light originates, and let Side 2 be the side that is behind the mirror. Having an object behind the mirror does not make sense; this case is not applicable.
| Sign Conventions | ||
|---|---|---|
| Measurement | Sign if on Side 1 | Sign if on Side 2 |
| s | + | N/A |
| i | + | - |
| f | + | - |
We shall see later that a modified version of these sign conventions also work for refracting surfaces.
In our picture where the source is between the focus and the reflector,

f > s, so that 1/f < 1/s. Hence, we need to subtract a quantity for the position equation to hold; making i negative is a convenient way of doing this. Note also that i's negativity shows that it is behind the mirror. The attentive reader can check that our sign conventions make sense for the other cases.
Now, looking at a convex mirror, we can easily find the magnification factor of a spherical mirror.
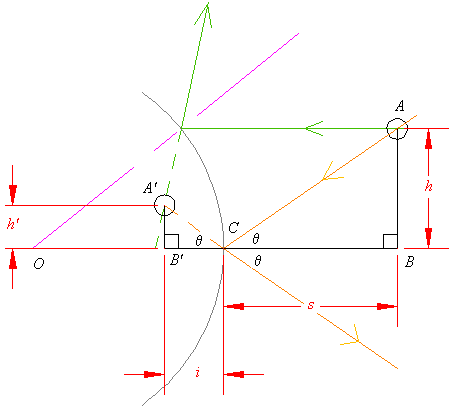
Dropping perpendiculars from the source and image points, and using the Law of Reflection, we see that the triangles ABC and A'B'C are similar. The magnification factor is exactly the ratio of the height of the image to the height of the source; the similar triangles give this ratio as h'/h = i/s, which can be found using the position formula. In fact, using the sign conventions mentioned above, if we use
for the magnification factor, the equation will also deal with inversion. If M is negative, the image will be inverted; if it is positive, the image is right side up.
We have developed many useful formulas in this section.
For a reflecting surface, let Side 1 be the side from which light originates, and let Side 2 be the side that is behind the mirror.
| Sign Conventions | ||
|---|---|---|
| Measurement | Sign if on Side 1 | Sign if on Side 2 |
| s | + | N/A |
| i | + | - |
| f | + | - |
Then, the positions of the image, source, and focus satisfy the equation
and the magnification of the image is given by
where M is negative for an inverted image, and positive for an upright one. We make these measurements starting from the reflecting surface.