In this section and the next, we will discuss mirrors, flat and curved. Many of the ideas explored in our discussion of mirrors will also be applicable in the realm of lenses.
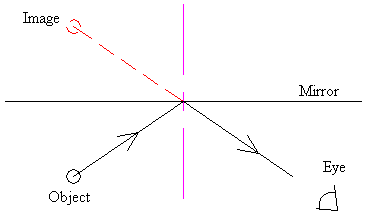
The simplest of mirrors are the flat ones; much of their function is explained using the Law of Reflection. Flat mirrors produce virtual images, images that cannot be caught and displayed in a screen. This is because there is no actual light coming from the image; what we see is the light from an object, reflected by the mirror.

The object is reflected in the mirror according to the Law of Reflection. The eye traces the reflected ray back to the image and sees it "behind" the mirror. The image is as far behind the mirror as the object is in front.
Simple plane geometry also shows us that all reflected rays from a point on an object can be traced back to the same image point.
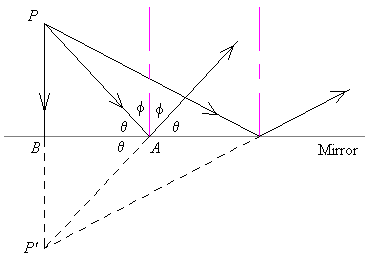
From an object point P, drop a perpendicular to the mirror, meeting at B. Construct a ray originating from P that strikes the mirror at A. Then, the Law of Reflection and elementary angle geometry shows us that the marked angles are equal. Using the common side and the right angles, the ASA theorem of congruent triangles shows that PBA and P'BA are congruent; the object is as far in front of the mirror as the image is behind. The ray reflected at A thus seems to originate from P'. Repeating the argument for other rays shows that all the reflected rays due to a point P on an object trace back to the same image point P'.
Many of the optical systems that we shall consider will consist of spherical arcs1. We first note that we can find the centre of any circular arc using elementary geometry.
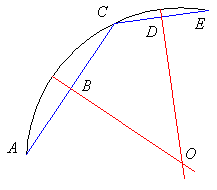
Any chord's perpendicular bisector passes through the arc's centre. Thus we can find the centre of an arc by constructing chords AC and CE and construct their perpendicular bisectors through B and D respectively. The intersection of the perpendicular bisectors is necessarily the centre of the arc, as such a centre is unique.
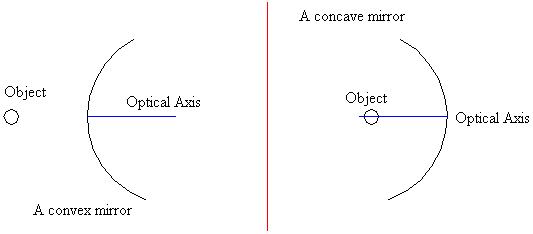
Spherical mirrors are classified according to their curvature. Concave mirrors bulge away from the objects they are reflecting, whereas convex mirrors bulge toward them. The optical axis of a spherical mirror is the line that joins its centre with the middle of the reflecting surface.
In our applications of lenses and mirrors, we will be very interested in light rays coming in from "infinity" which are parallel to the optical axis.
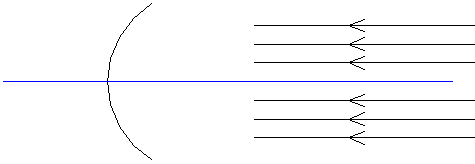
We can think of these light rays' source as being so far away that for all intents and purposes, the rays interacting with the optical system are parallel. In the study of optical systems, we will be mainly looking at the focus and the magnification of the systems. Also of importance is whether the image formed by the system is upright or inverted.