With apologies to the reader for horsing around à la Fermat, here is the proof.
We want to show that all rays coming in from infinity parallel to the axis of symmetry of a parabola get reflected onto the same point, the focus. Without loss of generality, consider a parabola of the form y = x2. The slope at any point is 2x.

If the focus exists, it must lie along the y-axis. A ray that comes in from infinity and hits a tangent of slope 1 will be reflected so that it travels horizontally (this follows from an application of the Law of Reflection for an angle of 45o). The point on the parabola with slope 1 has x-coordinate 1/2; hence if the focus exists, it has coordinates (0,1/22) = (0,1/4) = F.
Now consider any ray coming in from infinity, parallel to the axis of symmetry, and hitting the parabola at B.
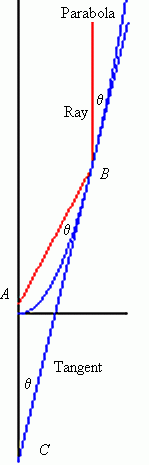
Using reflection and angle geometry of parallel lines, we see that we have an isosceles triangle in ABC. There is a unique point on the y-axis such that we get an isosceles. If we show that A is the focus, we are done. We can do this by showing BF2 = FC2; i.e. the squares of the distances are equal.
Let the ray come in with x-coordinate x0. Then B = (x0,x02). The tangent at B has slope 2x0. Using the point B, the point-slope form of the equation for the tangent tells us that the y-intercept has coordinate C = (0,-x02). Recall that F = (0,1/4). Then, using the square of the distances, we see
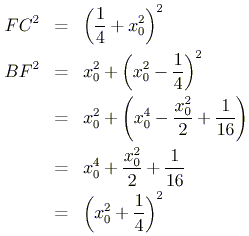
BF = FC, so that A = F. All rays coming in from infinity thus pass through the focus as calculated.
Back to discourse