|

In Orthographic projections, projections of parallels and meridians are
created by projecting from a point at infinite distance away from the
projection plane, which sit tangential to the other end of the diameter.
In the equatorial case, the light source comes from the west of the circle
at an infinite distance. As a result, the white rays radiating from that
infinite point willl appear to go through the earth parallel to each other
(as is the case of AB, CD and EF in Figure A). The projection plane CE
is situated tangentially to the east of the equator AB. Like other Zenithal
projections, one can think of the orthographic projection as being created
by the shadows casted upon the projection plane CE by the parallels and
meridians.
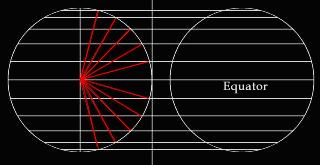
Figure B
When viewed in this perspective, parallels are seen as the horizontal
lines in Figure B, which is equivalent to the white lines in Figure C.
In both diagrams, the distance between two consecutive latitudes vary.
In fact, the parallels appear closer when further away from the equator.
The distances that the projected parallels are away from the equator is
as follows:
Given an arbitrary latitude DG in Figure A, it has the angular distance
<BOG away from the equator AB. Since the equator AB goes through
the centre of the earth and touches the tangential point B with the
plane CE, <CBO is a right angle. Therefore a line segment GH with
the same corresponding angle as <CBO (<GHO = <CBO) would make
GH and CB parallel lines intersected by another two parallel lines DG
and AB, implying that GH is equal to CB. Therefore the distance the
projected parallels are away from the equator is constructed using the
following trignometric relation:
- sin (<GOB) = GH/GO
- Since GO is the radius of the circle and <GOB is equivalent to
the angular distance the latitude is away from the equator GH=circle's
radius * sin (angular distance of latitude).
Therefore, the distance projected parallels are away from the centre
is equal to the circle's radius * sin (angular distance of latitude).
As such, as the latitudes increase, the distance between consecutive
parallels becomes smaller.
The meridians, on the other hand, are the vertical arcs seen in Figure
C. The derivation of such arcs are related to the parallels in that the
distribution of meridians along each parallels is equal to the distribution
of the parallels along the central meridian. This distribution can be
obtained by drawing a simple diagram as seen in Figure D. With the line
segment on the bottom of the triangle equivalent in length and division as that along the upper half
of the central meridian in Figure C, the radius of the latitudes are drawn
parallel to the base of the triangle and lined up at the height, which intersects the base perpendicularly.
Pick an arbitrary point along this vertical line (such as the point at the top of the triangle in
Figure D) to form the triangle as seen. Arrange the latitude's radius starting
with the smaller latitudes being closer to the base and touching the other two sides of the triangle.
The intersections obtained by drawing lines
from the top of the triangle to the divisions along the base would give proportional distribution
of meridians along each corresponding parallel. Therefore such lines are
representations of longitudes that increases in angular distance from
right to left. As a result, the sloped side of the triangle functions like the central meridian. Location
of meridians along the parallels can also be obtained mathematically.
As stated before, the radius of the parallels are equal to the circle's
radius * cos (angular distance of latitude) and since divisions along
the base are taken from the upper polar axis, this implies that the division
correspond to the relationship obtained above: circle's radius * sin (angular
distance of latitude). However, because the lines are representation of
longitudes, this means that the divisions are really circle's radius *
sin (angular distance of longitude) and since the radius changes each
time for each corresponding parallel the division of meridians along any
parallel becomes:
earth's radius * cos (angular distance of latitude) * sin (angular
distance of longitude).
|