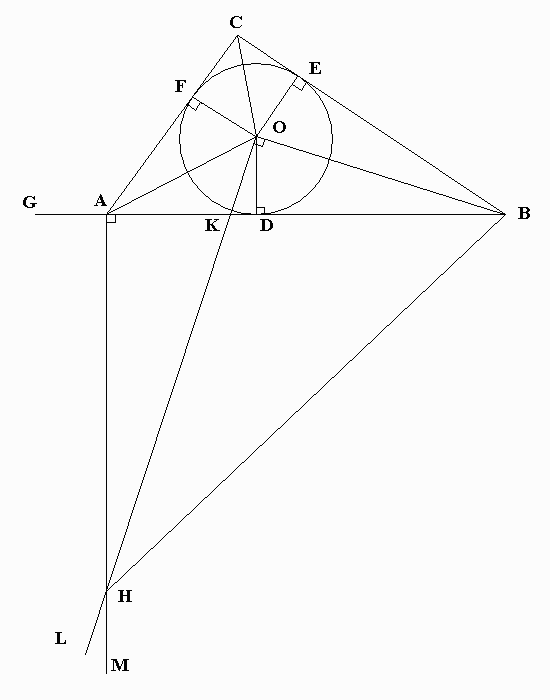Contents

Main Page

References and Links

Heron's Formula for Triangular Area

THEOREM

Figure 6

For a triangle having sides of length a, b, and c and area K, we have

K = sqrt[ s(s - a)(s - b)(s - c) ],
where s = ½(a + b + c) is the triangle's semi-perimeter.

PROOF

Let ABC be an arbitrary triangle. Also, let the side AB be at least as long as the other two sides (Figure 6).

Because the proof of Heron's Formula is "circuitous" and long, we'll divide the proof into three main parts.

Part A

Let O be the center of the inscribed circle. Let r be the radius of this circle (Figure 7). As we can see, OD = OE = OF = r.

Now, applying the usual formula for the area of triangles, we get:

Area(AOB) = ½(base)(height) = ½(AB)(OD) = ½cr

Area(BOC) = ½(base)(height) = ½(BC)(OE) = ½ar

Area(COA) = ½(base)(height) = ½(AC)(OF) = ½br

So,
K = Area(ABC) = Area(AOB) + Area(BOC) + Area(COA)
By substitution,
K = ½cr + ½ar + ½br = ½r(a + b + c) = rs

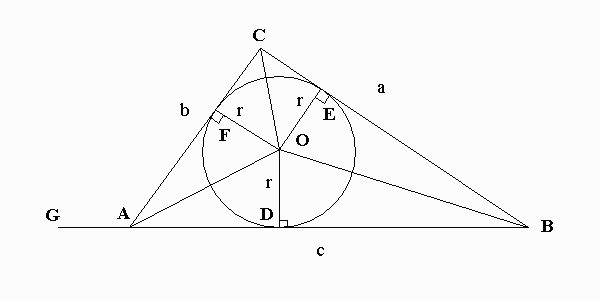Figure 7

Part B

Now, using Proposition 1, we can see that ABC is now made of three pairs of congruent triangles, namely
AOD is congruent to AOF
BOD is congruent to BOE
and
COE is congruent to COF
These congruences follow by AAS. Since corresponding parts of congruent triangles are congruent, we have
AD = AF, BD = BE, and CE = CF
while <AOD = <AOF, <BOD = <BOE, and <COE = <COF.

Now, extend the triangle's base AB to a point G, such that AG = CE. Now,

BG = BD + AD + AG = BD + AD + CE by construction

= ½(2BD + 2AD + 2CE)
= ½[(BD + BE) + (AD + AF) + (CE + CF)] by congruence
= ½[(BD + AD) + (BE + CE) + (AF + CF)]
= ½[AB + BC + AC]
= ½(c + a + b) = s

Now, since BG = s,

s - c = BG - AB = AG

s - b = BG - AC

= (BD + AD + AG) - (CF + AF)
= (BD + AD + CE) - (CE + AD) = BD since AF = AD, CF = CE and AG = CE.
Likewise,
s - a = BG - BC
= (BD + AD + AG) - (BE + CE)
= (BD + AD + CE) - (BD + CE) = AD since BD = BE and AG = CE.

These equalities just help us to visualize the segments s - a, s - b, and s - c.

Part C

Now, construct OL such that it's perpendicular to OB, intersecting AB at K (Figure 8).

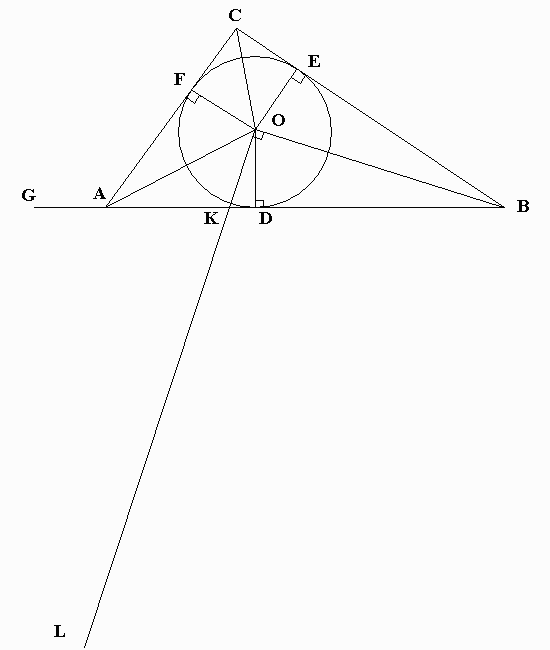Figure 8

Next, construct AM such that it's perpendicular to AB, intersecting OL at H (Figure 9).

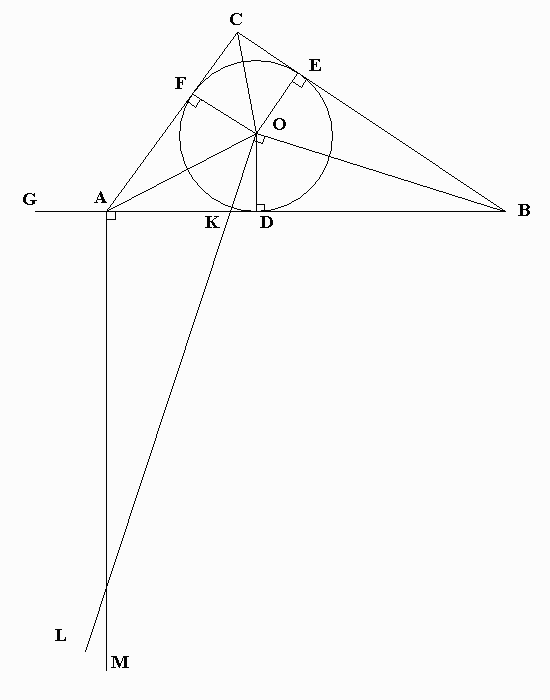Figure 9

Next, connect BH (Figure 10).

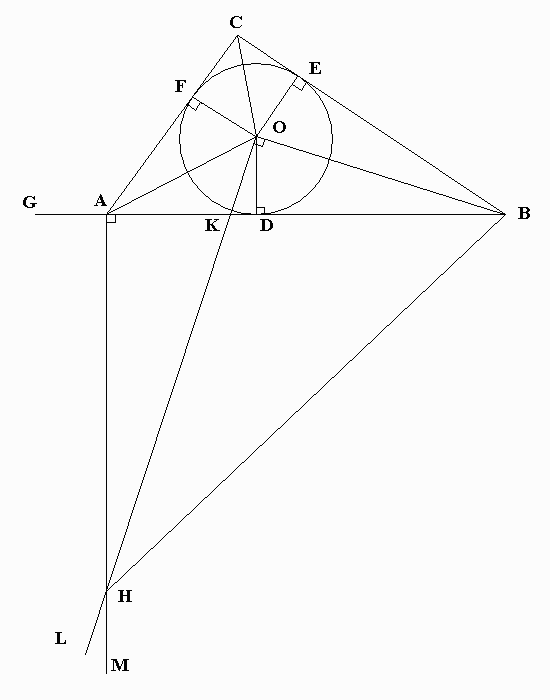Figure 10

By Proposition 4, the quadrilateral AHBO is a cyclic quadrilateral.

By Proposition 5, we know that <AHB + <AOB = 180 degrees. (*)

Please don't be discouraged with the following algebra. These can be visualized using Figure 10.

Now, let's focus on the angles about O.

From the congruences in part B, we see that
<FOA = <DOA, <DOB = <EOB, and <EOC = <FOC. (**)
Obviously,
<FOA + <DOA + <DOB + <EOB + <EOC + <FOC = 360 degrees.
By (**),
2<DOA + 2<DOB + 2<FOC = 360 degrees,
or
<DOA + <DOB + <FOC = 180 degrees. (***)

Obviously, <DOA + <DOB = <AOB. (****)

Substituting (****) into (***), we see that <AOB + <FOC = 180 degrees. (*****)
From (*) and (*****), <AHB = <FOC.

Now, we can see that triangle COF is similar to triangle BHA.

By similar triangles,
AB / AH = CF / OF = AG / r
since CF = AG and OF = r.

Equivalently,

AB / AG = AH / r (V*)

Similarly, triangle KAH is similar to KDO. This is because <KAH and <KDO are both 90 degrees, while <AKH = <DKO.

Again by similar triangles,
AH / AK = OD / KD = r / KD
Rearranging yields:
AH / r = AK / KD

Combining this with (V*), we get:

AB / AG = AK / KD (V**)
since both sides are equal to AH / r.

Now, look at triangle BOK. By Proposition 2, we see that triangle ODB and triangle KDO are similar.

By similar triangles, KD / r = r / BD
That is,
(KD)(BD) = r2 (V***)

Now, add 1 to both sides of (V**):

[AB / AG] + 1 = [AK / KD] + 1
Equivalently,
[AB + AG] / AG = [AK + KD] / KD
or
BG / AG = AD / KD

Multiplying this equation on the left by BG/BG and the right by BD/BD yields:

[(BG)(BG)] / [(AG)(BG)] = [(AD)(BD)] / [(KD)(BD)]
Substituting (V***) into this and simplifying, we get
[(BG)2] / [(AG)(BG)] = [(AD)(BD)] / [r2]
Cross-multiply:
r2(BG)2 = (AG)(BG)(AD)(BD)
Substituting the segments we derived in part B into the equation above, we get:
r2s2 = (s - c)(s)(s - a)(s - b) = s(s - a)(s - b)(s - c)
Therefore,
rs = sqrt[ s(s - a)(s - b)(s - c) ]

From Part A, the area of triangle ABC = K = rs.

This gives Heron's Formula:

K = sqrt[ s(s - a)(s - b)(s - c) ]