For a triangle having sides of length a, b, and c and area K, we have
We will try to prove Heron's formula the way Heron proved it. But before we begin the proof , we need to know a few preliminary results
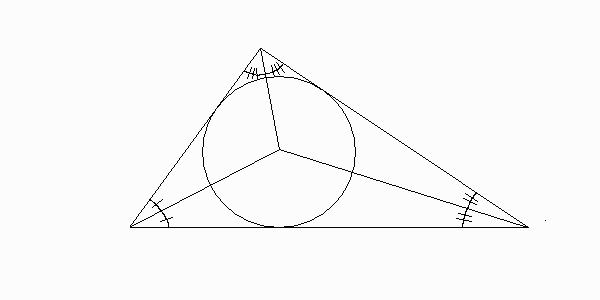
PROPOSITION 1 The bisectors of the angles of a triangle meet at a point that is the center of the triangle's inscribed circle. (Proposition IV.4 of Euclid's Elements)
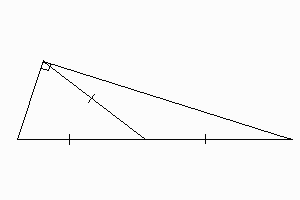
PROPOSITION 2 In a right-angled triangle, if a perpendicular is drawn from the right angle to the base, the triangles on each side of it are similar to the whole triangle and to one another. (Proposition VI.8 of the Elements)

PROPOSITION 3 In a right trangle, the midpoint of the hypotenuse is equidistant from the three vertices.
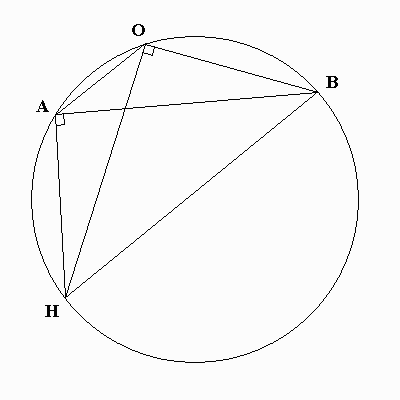
PROPOSITION 4 If AHBO is a quadrilateral with diagonals AB and OH, and if <HAB (angle HAB) and <HOB are right angles, then a circle can be drawn passing through the vertices A, O, B, and H.
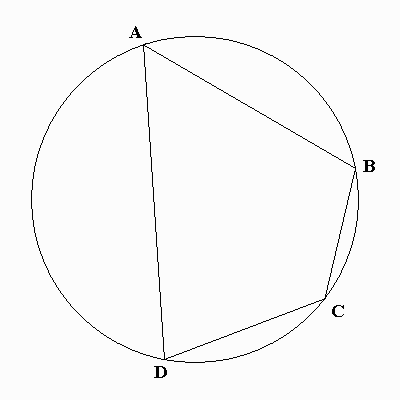
PROPOSITION 5 The opposite angles of a cyclic quadrilateral sum to 180 degrees. (Proposition III.22 of the Elements)