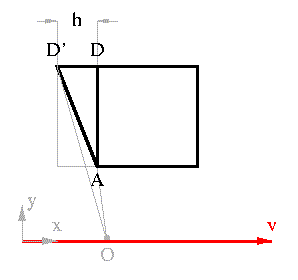
The previous analysis made the claim that light from D must travel an additional distance, l, compared with the distance the light must travel from A. This is the claim made by Terrell in his 1959 paper, but it assumes small angular separation. It is valid if the object is very small, or equivalently, if the observer is at infinity; the extra distance for the light to travel is negligible, and Terrell's result stands. However if the angular size is large, then it becomes significant -- see the picture; OD' is clearly longer than OD.

We could solve for h as follows: h=v(t_D' - t_A) where v is the velocity of the observer, t_D', the time for light to travel from D' and t_A similarly the time for light to travel from A. Where, t_A = OA/c (the length of OA), and T_D'= (OA - OD')/c and OD' is given by OD'=[ (y_A + l)^2 + (x_A + h)^2 ]^(1/2) with x_A and y_A the x and y components of OA. This becomes a quadratic in h that has real roots for small values of l compared with x_A.
But there is a nicer way to solve the problem. This method also explains the apparent curvature of lines perpendicular to the direction of motion, and the aberration of solid angle.