arbelos
What is an arbelos?
Properties of an arbelos
Distances and areas
Archimedes' circles
Apollonius circle
Bankoff circle
Pappus chain
References
Stephen Tan
42373027
Dec 16, 2005
Math 308 by Dr. Bill Casselman
Final Project
|
Archimedes' Book of Lemmas, Proposition V
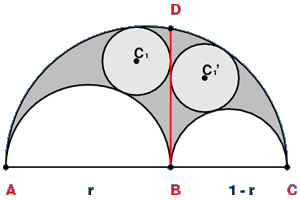
If two circles C1 and C1 are inscribed in the arbelos tangent to the line segment BD,
one on each side as shown in the figure, then the two circles are congruent.
Page 3, 4
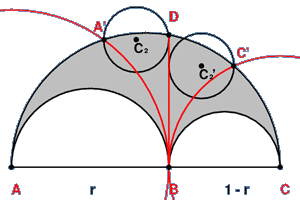
Archimedes' circles are circles inscribed in each half of the arbelos divided by BD and tangent to the arbelos.
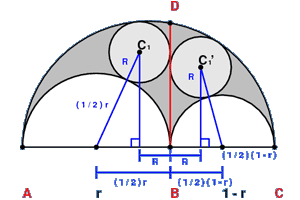
These circles are at centers C1 and C1' and has radii equal to r(1 - r)/2.
The positions of the circles can be found using the right triangles formed. By using the Pythagorean theorem, the centers can be calculated as so:
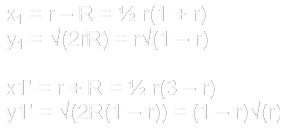
|
|
Page 5
Let A' be the point of intersection of a circle, centered at A with radius AB, and the circumference of the enclosing semicircle.
Likewise, let C' be the point of intersection of a circle, centered at C with radius BC, and the circumference of the enclosing semicircle.
The smallest circle, C2, passing through A' and tangent to BD is the equal to the smallest circle, C2', passing through C' and tangent to BD.
In additional to this, the radii R of these circles are equal to the radii of the Archimedes' circles.
To determine the position of C2, solve:
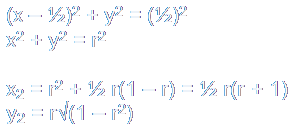
Similarly, to determine the position of C2', solve:
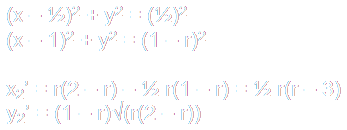
|
|
|