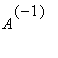 ?
?
Problem 7:
Let
![]() be the 20,000 x 20,000 matrix whose entries are zero everywhere except for the primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions
be the 20,000 x 20,000 matrix whose entries are zero everywhere except for the primes 2, 3, 5, 7, ..., 224737 along the main diagonal and the number 1 in all the positions
![]() with
with
![]() ,2,4,8,...,16384. What is the (1,1) entry of
,2,4,8,...,16384. What is the (1,1) entry of
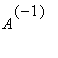 ?
?
Solution:
This is equivalent to computing
![]() after solving
after solving
![]() , where
, where
![]() . The system is diagonally dominant, and we use an iterative method:
. The system is diagonally dominant, and we use an iterative method:
 , where D is the diagonal of
, where D is the diagonal of
![]() (but without actually constructing the matrices). Gonnet used a Darwin program, equivalent to the following in Maple.
(but without actually constructing the matrices). Gonnet used a Darwin program, equivalent to the following in Maple.
| > | b:= Array(1..20000,datatype=float[8]): b[1]:= 1: x:= Array(1..20000,datatype=float[8]): primes:= Array(1..20000,datatype=float[8]): for i from 1 to 20000 do primes[i]:= ithprime(i) od: |
| > | solvproc:= proc(N) local iter, toterr, i, rhs, ij, newxi; global x; for i from 1 to N do x[i]:= 0 od: for iter to 40 do toterr := 0; for i to N do rhs := b[i]; ij := 1; while ij < N do if i-ij > 0 then rhs := rhs - x[i-ij] fi; if i+ij <= N then rhs := rhs - x[i+ij] fi; ij := 2*ij od; newxi := rhs/primes[i]; toterr := toterr + abs(newxi-x[i]); x[i] := newxi od; if toterr=0 then break fi; lprint(toterr); od: x[1]; end; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | ti:= time(): evalhf(solvproc(20000)); (time()-ti)*seconds ; |
.887865995381123986
.278658134431981340
.873116873307076269e-1
.280984403047528780e-1
.896168412303717000e-2
.282597754444424655e-2
.885708717267995350e-3
.276700748083163562e-3
.862812417589902238e-4
.268719686136664988e-4
.836254516891092076e-5
.260111747308844605e-5
.808810146402529806e-6
.251448343535394878e-6
.781623535215165102e-7
.242947694034407002e-7
.755103880822366756e-8
.234685997925699352e-8
.729389779125172184e-9
.226686206265103620e-9
.704513858008347722e-10
.218954121769508914e-10
.680502535422857584e-11
.211472595988469877e-11
.656998092145587618e-12
.204068598900091197e-12
.635341005751694184e-13
.199326919187803528e-13
.616146405998221652e-14
.163608756217164570e-14
.409211670512742128e-15
.708330759345821984e-16
.934890384403199346e-19
.545716338525474910e-22
.355549011630070350e-29
.173686262298320443e-34
![]()
![]()
This answer is correct to 14 digits.