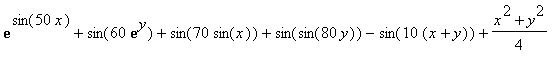 ?
?
What is the global minimum of the function
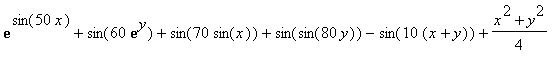 ?
?
Solution:
Look at the function for reasonably small values of x and y.
| > | restart; F := (x,y) -> exp(sin(50*x)) + sin(60*exp(y)) + sin(70*sin(x)) + sin(sin(80*y)) - sin(10*(x+y)) + 1/4*(x^2+y^2); |
![]()
![]()
| > | plot3d(F(x,y),x=-2..2,y=-2..2,axes=box,grid=[100,100],style=patchcontour,shading=ZHUE); |
![[Maple Plot]](images/challenge177.gif)
It looks like a nightmare for someone trying to find the global minimum: there are huge numbers of local minima. Note however that there's an easy lower bound:
 . From the graph it looks like there are points where F(x,y) is below -2. In fact, the minimum value plotted is
. From the graph it looks like there are points where F(x,y) is below -2. In fact, the minimum value plotted is
| > | P:= %: |
| > | G:= op([1,3],P); |

| > | CurrMin:=min(seq(seq(G[i,j],i=1..100),j=1..100)); |
![]()
For any point doing better than that,
 so
so

| > | rmax:=sqrt(4*(CurrMin+4-exp(-1.0))); |
![]()
So we certainly don't have to search farther away from the origin than that. Now suppose we search in a rectangular grid such that every point
![]() in the disk of radius
in the disk of radius
![]() in the
in the
![]() direction and
direction and
![]() in the
in the
![]() direction of a grid point
direction of a grid point
![]() . If
. If
![]() is the actual minimum (so in particular
is the actual minimum (so in particular
![]() ), how much bigger than
), how much bigger than
![]() can
can
![]() be? Well, from Taylor's Theorem (remembering that the first derivatives of
be? Well, from Taylor's Theorem (remembering that the first derivatives of
![]() at the minimum are 0),
at the minimum are 0),
![]()
![F(x[i],y[j]) = F(x[0],y[0])+F[x,x](x,y)*(x[i]-x[0])^2/2+F[x,y](x,y)*(x[i]-x[0])*(y[j]-y[0])+F[y,y](x,y)*(y[j]-y[0])^2/2](images/challenge197.gif) for some point
for some point
![]() on the line segment from
on the line segment from
![]() to
to
![]() . In particular if
. In particular if
![]() ,
,
![]() and
and
![]() , we have
, we have
![F(x[i],y[j]) <= CurrMin+a*dx^2/8+b*dx*dy/4+c*dy^2/8](images/challenge204.gif) .
.
| > | a:= op([1,2],evalf(evalr(subs(x=INTERVAL(-rmax..rmax),y=INTERVAL(-rmax..rmax),diff(F(x,y),x$2))))); |
![]()
| > | b:= op([1,2],evalf(evalr(subs(x=INTERVAL(-rmax..rmax),y=INTERVAL(-rmax..rmax),abs(diff(F(x,y),x,y)))))); |
![]()
| > | c:= op([1,2],evalf(evalr(subs(x=INTERVAL(-rmax..rmax),y=INTERVAL(-rmax..rmax),diff(F(x,y),y,y))))); |
![]()
With dx = .006 and dy = .002, I get
| > | dz:=eval(a*dx^2/8 + b*dx*dy/4 + c*dy^2/8,{dx=.006,dy=.002}); |
![]()
| > | ti:= time(): dx:= .006: dy:= .002: candidates:= NULL; imax:= ceil(rmax/dx); for i from -imax to imax do xi:= i*dx; if abs(xi) > rmax then jmax:= 1 else jmax:= ceil(sqrt(rmax^2-xi^2)/dy) fi; for j from -jmax to jmax do yj:= j*dy; Fij:= evalhf(F(xi,yj)); if Fij < CurrMin + dz then candidates:= candidates,[xi,yj,Fij]; if Fij < CurrMin then CurrMin:= Fij; bestcand:= [xi,yj]; fi fi od od: (time()-ti)*seconds; |
| > |
![]()
![]()
![]()
| > | nops([candidates]); |
![]()
| > | CurrMin; |
![]()
We've come down quite a bit from the previous CurrMin. Now we can search closer to each of the 75 candidates.
| > | dx:= .0006; dy:= .0002; dz:= a*dx^2/8 + b*dx*dy/4 + c*dy^2/8;candidates2:= NULL: |
![]()
![]()
![]()
| > | ti:= time(): for cand from 1 to 75 do for i from -5 to 4 do xi:= candidates[cand][1]+(i+1/2)*dx; for j from -5 to 4 do yj:= candidates[cand][2]+(j+1/2)*dy; Fij:= evalhf(F(xi,yj)); if Fij < CurrMin + dz then candidates2:= candidates2,[xi,yj,Fij]; if Fij < CurrMin then CurrMin:= Fij; bestcand:= [xi,yj]; fi fi od od od: (time()-ti)*seconds; |
![]()
| > | nops([candidates2]); |
![]()
| > | candidates2; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | plots[display]({ plots[implicitplot](diff(F(x,y),x),x=-.0255-dx/2 .. -.0237+dx/2, y=0.2099-dy/2 .. 0.2111+dy/2, colour=red), plots[implicitplot](diff(F(x,y),y),x=-.0255-dx/2 .. -.0237+dx/2, y=0.2099-dy/2 .. 0.2111+dy/2, colour=blue) }); |
![[Maple Plot]](images/challenge235.gif)
| > | Digits:= 30; fsolve({diff(F(x,y),x), diff(F(x,y),y)},{x,y},x=-.0255-dx/2 .. -.0237+dx/2, y=0.2099-dy/2 .. 0.2111+dy/2); |
![]()
![]()
![]()
| > | eval(F(x,y),%); |
![]()
All 30 digits here are correct.