Problem 2:

A photon moving at speed 1 in the plane starts at at heading due east. Around every integer lattice point in the plane, a circular mirror of radius has been erected. How far from the origin is the photon at ?

Solution:

You have to be careful to use enough digits here, because there are 13 reflections, and each reflection from a curved surface amplifies the error. We needed 11 additional digits.

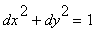The state of the photon is where is the position, the velocity, the distance travelled. We always have dx^2+dy^2 = 1 .

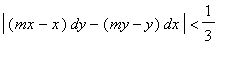
Starting in this state, you hit a mirror centred at if abs((mx-x)*dy-(my-y)*dx) < 1/3

(assuming that mirror is in the forward direction, and you don't hit anything else first).

If so, let be the point where it hits. This is where

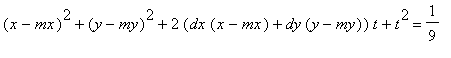(x-mx)^2+(y-my)^2+2*(dx*(x-mx)+dy*(y-my))*t+t^2 = 1/9 . Then the next state is

where .

> plots[display]([plottools[circle]([0,0],1), plots[arrow]([2,-2],[-1,2],shape=arrow,colour=blue),
plots[arrow]([1,0],[1,2],shape=arrow,colour=blue),
plots[arrow]([1,0],[2,0],shape=arrow,colour=red)
],axes=none,scaling=constrained);

[Maple Plot]

Global variables: x, y, dx, dy, s for current state;
if going mainly in direction, iy = 0 and ix is integer to go in direction to next mirror;

if going mainly in direction, ix = 0 and iy is integer to go in direction to next mirror.

>    move:= proc()
# return true if you hit the mirror or end of path
# and update state in this case,
# false if you don't (leaving state unchanged)
  local mx, my, t, px, py,h,ds;
  global x,y,dx,dy,s,ix,iy;
  if iy = 0 then # going in x direction
    mx:= round(x+ix-.001);
    my:= round(y+dy/dx*ix);
    ds:= sqrt(1+(dy/dx)^2)*abs(mx-x);
  else # going in y direction
    my:= round(y+iy);
    mx:= round(x+dx/dy*iy);
    ds:= sqrt(1+(dx/dy)^2)*abs(my-y);
  fi;
  if abs((mx-x)*dy - (my-y)*dx) < 1/3 then
    t:= min(fsolve((x+t*dx-mx)^2 + (y+t*dy-my)^2=1/9,t));
    px:= x+t*dx; py:= y+t*dy;
    ds:= sqrt((px-x)^2+(py-y)^2);
    if s + ds >= 10 then
      x:= x + (10-s)*dx;
      y:= y + (10-s)*dy;
      s:= 10;
      return true;
    else
      h:= 18*((mx-px)*dx+(my-py)*dy);
      s:= s + ds;
      dx:= dx - h*(mx-px);
      dy:= dy - h*(my-py);
# dx^2 + dy^2 should stay constant, but make sure
      h:= sqrt(dx^2+dy^2);
      dx:= dx/h; dy:= dy/h;
      x:= px; y:= py;
      return true;
    fi
  # no hit, but maybe we'd go too far
  elif s + ds >= 10 then
    x:= x + (10-s)*dx;
    y:= y + (10-s)*dy;
    s:= 10;
    return true;
  fi;
false
end;

Initial conditions.

> x,y,dx,dy,s:= 0.5, 0.1, 1, 0, 0; path:= [x,y]; ix:= 1; iy:= 0;
_Envsignum0:= 0; Digits:= 50;

>    while s < 10 do
  if move() then # reassess directions
    if abs(dx) >= abs(dy) then
      ix:= signum(dx); iy:= 0
    else
      ix:= 0; iy:= signum(dy);
    fi;
    path:= path,[x,y];
  else # go to next mirror in same direction
    ix:= ix+signum(ix);
    iy:= iy+signum(iy);
  fi
od:

The final state:

> x,y,dx,dy,s;

The answer:

> ans:=sqrt(x^2+y^2);

> with(plots): display({plot([path]),seq(seq(plottools[circle]([i,j],1/3),i=-1..1),j=-1..2)},scaling=constrained,axes=frame);

Warning, the name changecoords has been redefined

[Maple Plot]

Just for comparison, here it is with 40 digits.

>    x,y,dx,dy,s:= 0.5, 0.1, 1, 0, 0: path:= [x,y]: ix:= 1: iy:= 0:
_Envsignum0:= 0: Digits := 40:
while s < 10 do
  if move() then # reassess directions
    if abs(dx) >= abs(dy) then
      ix:= signum(dx); iy:= 0
    else
      ix:= 0; iy:= signum(dy);
    fi;
    path:= path,[x,y];
  else # go to next mirror in same direction
    ix:= ix+signum(ix);
    iy:= iy+signum(iy);
  fi
od:
ans40:= sqrt(x^2+y^2);

> ans40 - ans;

And here's what we would have got with a starting point different by 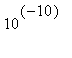10^(-10) in the y direction.

>    path0:= path:
x,y,dx,dy,s:= 0.5, 0.1+1e-10, 1, 0, 0: path:= [x,y]: ix:= 1: iy:= 0:
_Envsignum0:= 0: Digits := 40:
while s < 10 do
  if move() then # reassess directions
    if abs(dx) >= abs(dy) then
      ix:= signum(dx); iy:= 0
    else
      ix:= 0; iy:= signum(dy);
    fi;
    path:= path,[x,y];
  else # go to next mirror in same direction
    ix:= ix+signum(ix);
    iy:= iy+signum(iy);
  fi
od:

> display({plot([path],colour=blue),plot([path0],colour=red),seq(seq(plottools[circle]([i,j],1/3),i=-1..1),j=-1..2)},scaling=constrained,axes=frame);

[Maple Plot]