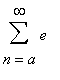 converges (where
converges (where
Function: csum - check convergence of a series
Calling sequence:
csum(e,n);
Parameters:
e - an expression (the summand), depending on n
n - a name
Description:
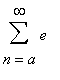 converges (where
converges (where
Examples:
A typical convergent series.
> csum(1/(n^2+1),n);
![]()
A typical divergent series.
> csum((n^2+1)/(n^3+1),n);
![]()
A series that converges conditionally. Setting infolevel[csum] gives us extra information.
>
infolevel[csum]:= 1;
csum(exp(I*n)/ln(n),n);
![]()
csum: Checking sum of exp(I*n)/ln(n) over n
csum: Series does not converge absolutely
csum/condit: Series converges
![]()
A series whose convergence is an open question (involving how well
![]() can be represented by rational numbers). Not surprisingly,
csum
can't decide it.
can be represented by rational numbers). Not surprisingly,
csum
can't decide it.
>
infolevel[csum]:= 0:
csum(1/(n^4*sin(n)^2),n);
![]()
Bugs in limit can affect csum . In this case the bug produces an incorrect result in the ratio test. This one should diverge.
>
infolevel[csum]:= 2:
csum(sin(n)/2^n+1/n,n);
csum: Checking sum of sin(n)/(2^n)+1/n over n
csum/limitzero: Checking limit of terms
csum/limitzero: OK, limit is 0
csum/ratiotest: Trying ratio test
csum/ratiotest: Ratio test succeeds with ratio limit 0
csum: Series sin(n)/(2^n)+1/n converges absolutely
![]()
> limit((sin(n+1)/2^(n+1)+1/(n+1))/(sin(n)/2^n+1/n),n=infinity);
![]()
A series depending on a parameter
![]() . Convergence depends on the value of
. Convergence depends on the value of
![]() .
.
> csum(p^n/n,n);
![]()
This one converges for all
![]() .
.
> csum(p^n/n!,n);
![]()
With an assumption:
> assume(p>-1,p<1): csum(p^n/n,n);
![]()
This one diverges for
![]() , but
csum
does not catch that.
, but
csum
does not catch that.
> csum(1/(n+p*n^2),n);
![]()
See also:
assume , limit , sum
Maple Advisor Database R. Israel 2000