Bug fix: Bugs in definite and IsDefinite
Examples:
> with(linalg,definite,eigenvalues): with(LinearAlgebra,IsDefinite):
A symmetric, but not hermitian matrix, should not be considered (any type of) definite. This one's eigenvalues are not even real. But both
definite
and
IsDefinite
return
![]() .
.
>
A1:= matrix([[1,I],[I,2]]);
definite(A1,positive_def);
IsDefinite(Matrix(A1),query=positive_def);
eigenvalues(A1);
![A1 := matrix([[1, I], [I, 2]])](images/b13r4.gif)
![]()
![]()
![]()
A hermitian, but not symmetric matrix. This should be positive definite, but
definit
e returns
![]() .
.
>
A2:= matrix([[1,-I],[I,2]]);
definite(A2,positive_def);
IsDefinite(Matrix(A2),query=positive_def);
eigenvalues(A2);
![A2 := matrix([[1, -I], [I, 2]])](images/b13r9.gif)
![]()
![]()
![]()
This matrix is hermitian (if the symbolic parameter
![]() is real). Again
definite
returns
is real). Again
definite
returns
![]() , and this time
IsDefinite
returns an error. The correct answer is that this is positive definite if
, and this time
IsDefinite
returns an error. The correct answer is that this is positive definite if
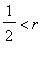 .
.
>
A3:= matrix([[r,-I],[I,2]]);
definite(A3,positive_def);
IsDefinite(Matrix(A3),query=positive_def);
eigenvalues(A3);
![A3 := matrix([[r, -I], [I, 2]])](images/b13r16.gif)
![]()
Error, (in LinearAlgebra:-LA_Main:-IsDefinite) cannot evaluate boolean: -r < 0 and -2*r < -1
![]()
> solve(1/2*r+1-1/2*sqrt(r^2-4*r+8)>0);
![]()
Here is an example of a real symmetric matrix which produces incorrect results in IsDefinite with query=positive_semidef . Its diagonal entries are positive, but the matrix is not positive semidefinite, in fact the determinant is negative.
>
A4:= matrix([[1,1,5],[1,1,1],[5,1,1]]);
definite(A4,positive_semidef);
IsDefinite(Matrix(A4),query=positive_semidef);
linalg[det](A4);
![A4 := matrix([[1, 1, 5], [1, 1, 1], [5, 1, 1]])](images/b13r20.gif)
![]()
![]()
![]()
Here is an example of a real symmetric matrix which produces incorrect results in both definite and IsDefinite because of a mathematical error: these procedures don't check determinants of principal submatrices for non-contiguous rows and columns (in this case rows and columns 1 and 3).
>
A5:= matrix([[1,0,2],[0,0,0],[2,0,1]]);
![A5 := matrix([[1, 0, 2], [0, 0, 0], [2, 0, 1]])](images/b13r24.gif)
This matrix has both positive and negative eigenvalues.
> linalg[eigenvalues](A5);
![]()
However, it tests as positive semidefinite, and -A5 tests as negative semidefinite. Here it is using the linalg package's definite :
>
linalg[definite](A5,positive_semidef);
linalg[definite](evalm(-A5),negative_semidef);
![]()
![]()
And here it is using the LinearAlgebra package's IsDefinite :
>
AM:= Matrix(A5):
LinearAlgebra:-IsDefinite(AM,query=positive_semidef);
LinearAlgebra:-IsDefinite(-AM,query=negative_semidef);
![]()
![]()
All of these work correctly using the Maple Advisor Database function semidef .
>
`A1: `,semidef(A1,positive_def);
`A2: `,semidef(A2,positive_def);
`A3: `,semidef(A3,positive_def);
`A4: `,semidef(A4,positive_semidef);
`A5: `,semidef(A5,positive_semidef);
`-A5: `,semidef(evalm(-A5),negative_semidef);
`AM: `,semidef(AM,positive_semidef);
`-AM: `,semidef(-AM,negative_semidef);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
See also:
definite , IsDefinite , linalg , LinearAlgebra , semidef
Maple Advisor Database R. Israel 2000