Bug fix: Residue returns 0

The function residue computes the residue of an analytic function at a pole of the function.

> residue(sin(z)/z^2,z=0);

In some cases residue returns an incorrect answer of 0.

> f:= x/(1+x^7): p:= cos(Pi/7)+I*sin(Pi/7):
residue(f,x=p);

> pr:= RootOf(1+Z^7);
residue(f,x=pr);

This is usually due to the series command not recognizing that the denominator is 0 at the given point.

> series(f,x=p,1);

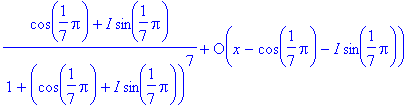
> series(f,x=pr,1);

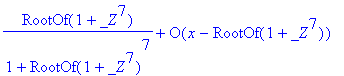
Sometimes this problem can be helped by using a different representation of the point . In this case using complex exponentials instead of sines and cosines would work.

> residue(f,x=convert(p,exp));

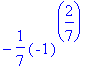
Another possibility which sometimes works is to change the environment variable Testzero , whose value is the procedure used in series to determine when the leading coefficient is 0. By default this uses Normalizer , another environment variable whose default value is normal . Since residue and series have the remember option, we must use forget to remove results obtained using Normalizer from their remember tables.

> Testzero:= proc(O) evalb(simplify(O)=0) end:
forget(series);
forget(residue);
residue(f,x=pr);

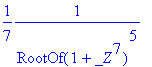
However, this does not work in the case of our .

> residue(f,x=p);

Another way this problem can arise is when you have a floating-point approximation to a singularity rather than an actual singularity.

> pf:= evalf(p);

> residue(f,x=pf);

In this case it's arguably not Maple's fault: the given point is not actually a singularity of , but only an approximation of a singularity. At itself, has a finite (though large) value.

> eval(f,x=pf);

If you know that should have a simple pole at the given point, you may be able to calculate the residue "by hand". For example:

> eval(numer(f)/diff(denom(f),x),x=p);

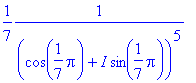
> eval(numer(f)/diff(denom(f),x),x=pf);

Maple Advisor Database, R. Israel 2000