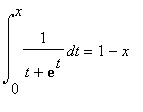 . Using calculus, it is not hard to prove that this has exactly one solution with
. Using calculus, it is not hard to prove that this has exactly one solution with
Advice: Solving equations involving numerical integration
Suppose you want to solve an equation involving a function
![]() , defined as a definite integral which Maple must evaluate numerically. For example, you might want to solve the equation
, defined as a definite integral which Maple must evaluate numerically. For example, you might want to solve the equation
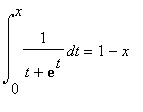 . Using calculus, it is not hard to prove that this has exactly one solution with
. Using calculus, it is not hard to prove that this has exactly one solution with
![]()
![]() . It is convenient to write the equation as
. It is convenient to write the equation as
![]() :
:
> F:= x -> Int(1/(t + exp(t)), t=0..x) + x;
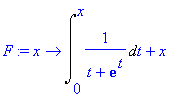
We use the inert form Int rather than int , because int(1/(t+exp(t)), t=0..x) returns unevaluated. Now we can solve the equation numerically:
> fsolve(F(x)=1, x = 0 .. 1);
![]()
This takes a rather long time to solve, since it requires evaluating the function
![]() at many points, and each such evaluation requires another numerical integration. But another approach, based on differential equations, can be used. Note that
at many points, and each such evaluation requires another numerical integration. But another approach, based on differential equations, can be used. Note that
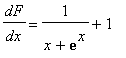 , with
, with
![]() . Now since
. Now since
![]() is a one-to-one function of
is a one-to-one function of
![]() , we can just as well consider
, we can just as well consider
![]() as a function of
as a function of
![]() . It will satisfy the differential equation
. It will satisfy the differential equation
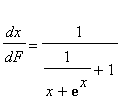 with initial condition
with initial condition
![]() , and what we want is
, and what we want is
![]() .
.
> de:= diff(x(F),F) = 1/(1/(x(F)+exp(x(F)))+1);
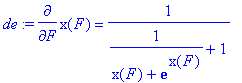
> soln:= dsolve({de, x(0)=0},x(F), numeric);
![]()
> soln(1);
![]()
This approach would not work in more general cases, e.g. an integral depending on a parameter whose value must be found. In those cases the solution must be found with fsolve .
See also: fsolve , dsolve/numeric
Maple Advisor Database, R. Israel 1997