
Euclid: Picture courtesy of Lexington High School

Euclid: Picture courtesy of Lexington High
School
Leanna Ho and Laura Keating
Student # (82708017) and (84323013)
MATH 308, Bill Casselman
Final Project
Table of
Contents:
The Construction of a Regular Icosahedron
The Proof of Regularity
Symmetry
Related Proofs
References
The Construction of a Regular Icosahedron - Euclid Book
XIII Proposition 16
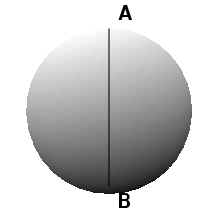 The diameter of a given sphere is AB.
The diameter of a given sphere is AB.
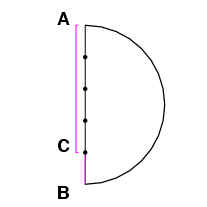 Cut the diameter, AB, at C so that AC is quadruple CB. [Book VI Proposition 9][Book I Proposition 11]
Cut the diameter, AB, at C so that AC is quadruple CB. [Book VI Proposition 9][Book I Proposition 11]
 The semicircle ADB is described, such that a straight line CD is drawn from C at a right angle
to AB. Join DB.
The semicircle ADB is described, such that a straight line CD is drawn from C at a right angle
to AB. Join DB.
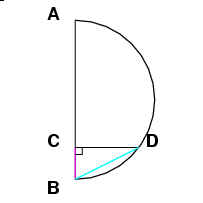
 Let the diameter of a circle be DB
Let the diameter of a circle be DB
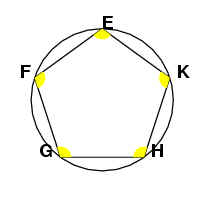 Inscribe the equilateral and equilangular pentagon EFGHK in the circle.
Inscribe the equilateral and equilangular pentagon EFGHK in the circle.
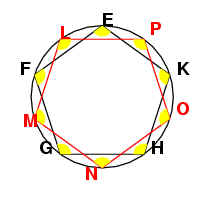 Bisect the circumferences EF, FG, GH and KE at the points L, M, N, O and
P. (see bisecting angles proof -postscript file) Join these points to form an
equilateral equiangular pentagon.
Bisect the circumferences EF, FG, GH and KE at the points L, M, N, O and
P. (see bisecting angles proof -postscript file) Join these points to form an
equilateral equiangular pentagon.
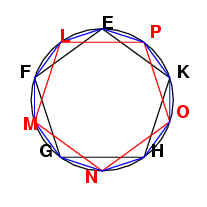 The straight line GN belongs to a
decagon.
The straight line GN belongs to a
decagon.
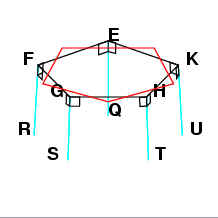 Set up straight lines EQ, RF, GS, HT and KU at right angles to the
plane of the circle, and make these lines equal to the radius of circle EFGHK
(ie. equal to BD from the first circle). [Book XI Proposition 12]
Set up straight lines EQ, RF, GS, HT and KU at right angles to the
plane of the circle, and make these lines equal to the radius of circle EFGHK
(ie. equal to BD from the first circle). [Book XI Proposition 12]
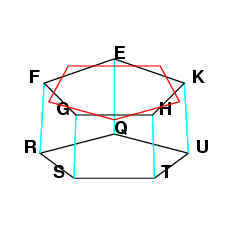 Join QR, RS, ST, TU and UQ. Since
each of the straight lines EQ and KU is at right angles to the same plane, then
EQ is parallel to KU[Book IV Proposition 11].ps">Book I Proposition 33]. Since they are also equal to the radius of circle EFGHK,
they are also equal. Since EK is belongs to an equilateral pentagon, QU also
belongs to the equilateral pentagon inscribed inside the circle EFGHK. Following
the same reasoning, QR, RS, ST and TU also belong to the equilateral pentagon
inscribed inside EFGHK, and therefore QRSTU is an equilateral pentagon.
Join QR, RS, ST, TU and UQ. Since
each of the straight lines EQ and KU is at right angles to the same plane, then
EQ is parallel to KU[Book IV Proposition 11].ps">Book I Proposition 33]. Since they are also equal to the radius of circle EFGHK,
they are also equal. Since EK is belongs to an equilateral pentagon, QU also
belongs to the equilateral pentagon inscribed inside the circle EFGHK. Following
the same reasoning, QR, RS, ST and TU also belong to the equilateral pentagon
inscribed inside EFGHK, and therefore QRSTU is an equilateral pentagon.
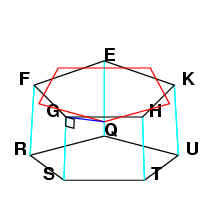 Join SN. GS belongs to a hexagon and GN belongs to a decagon, therefore SGN is a
right angle.
Join SN. GS belongs to a hexagon and GN belongs to a decagon, therefore SGN is a
right angle.
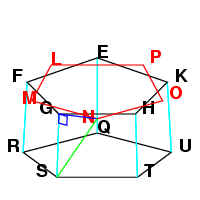 Since the square of the side of the pentagon equals the sum of the
square on the side of the hexagon plus the square on the side of the decagon
inscribed inside the same circle [Book XIII Proposition 10], therefore SN belongs to a
pentagon.
Since the square of the side of the pentagon equals the sum of the
square on the side of the hexagon plus the square on the side of the decagon
inscribed inside the same circle [Book XIII Proposition 10], therefore SN belongs to a
pentagon.
 For the same reason, NT belongs to a pentagon. Since we already
know that ST belongs to a pentagon, therefore SNT is an equilateral triangle.
For the same reason, NT belongs to a pentagon. Since we already
know that ST belongs to a pentagon, therefore SNT is an equilateral triangle.
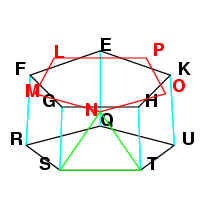
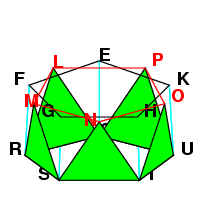 Joining QL, LR, RM, MS, SN, NT, TO, OU, UP and PQ, we can show by the same
reasoning that triangles QLR, RSM, QPU and TOU are equilateral.
Joining QL, LR, RM, MS, SN, NT, TO, OU, UP and PQ, we can show by the same
reasoning that triangles QLR, RSM, QPU and TOU are equilateral.
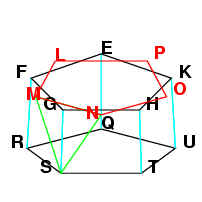 Since we also already showed that SN and SM both belong to a pentagon, and MN belongs to
pentagon LMNOP, then MSN is also an equilateral triangle.
Since we also already showed that SN and SM both belong to a pentagon, and MN belongs to
pentagon LMNOP, then MSN is also an equilateral triangle.
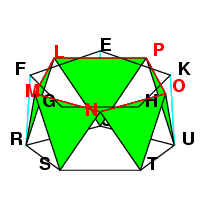 By the same reasoning as before, triangles LRM, QLP, NTO and OUP are also
equilateral.
By the same reasoning as before, triangles LRM, QLP, NTO and OUP are also
equilateral.
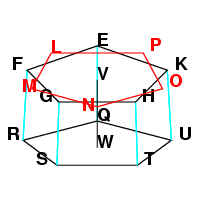 Take the centre, V, of the circle EFGHK and the centre, W, of
the circle that pentagon QRSTU would be inscribed in. VW is the length of a
hexagon.
Take the centre, V, of the circle EFGHK and the centre, W, of
the circle that pentagon QRSTU would be inscribed in. VW is the length of a
hexagon.
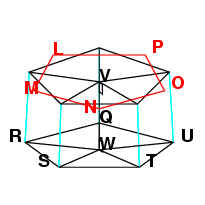 Since VW is at a right angle with the plane of the circle, then VW
is parallel to QE. They are also equal. Therefore EV and QW are also equal and
parallel [Book I Proposition 33]
Since VW is at a right angle with the plane of the circle, then VW
is parallel to QE. They are also equal. Therefore EV and QW are also equal and
parallel [Book I Proposition 33]
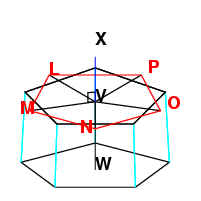 Extend VW by the length of the decagon, to VX. VX is at a
right angle to the plane of the circle EFGHK.
Extend VW by the length of the decagon, to VX. VX is at a
right angle to the plane of the circle EFGHK.
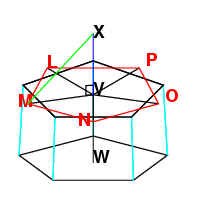 Since VM belongs to a hexagon,
and VX belongs to a decagon, the angle MVX is right, and therefore MX belongs to
a pentagon.
Since VM belongs to a hexagon,
and VX belongs to a decagon, the angle MVX is right, and therefore MX belongs to
a pentagon.
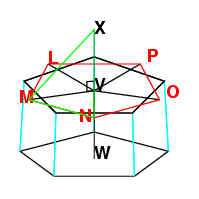 Joining NX, by the same reasoning NX belongs to a pentagon.
Since we know MN already belongs to a pentagon, then MNX is an equilateral
triangle.
Joining NX, by the same reasoning NX belongs to a pentagon.
Since we know MN already belongs to a pentagon, then MNX is an equilateral
triangle.
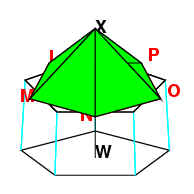 Similarly, the triangles NOX, OPX, PLX and LMX are equilateral by
the same reasoning.
Similarly, the triangles NOX, OPX, PLX and LMX are equilateral by
the same reasoning.
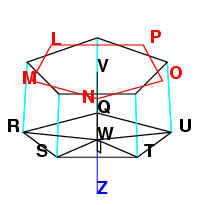 We extend VW by the length of a decagon in the other
direction this time, to get WZ. WZ is at a right angle from the plane of the
pentagon QRSTU, and WZ belongs to a decagon.
We extend VW by the length of a decagon in the other
direction this time, to get WZ. WZ is at a right angle from the plane of the
pentagon QRSTU, and WZ belongs to a decagon.
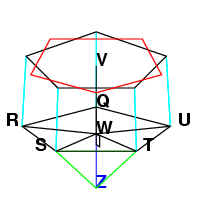 Since JV belonged to a hexagon,
then SW, which is equal and parallel to SV, also belongs to a hexagon. WZ
belongs to a decagon and SWZ is a right angle, therefore SZ belongs to a
pentagon. Then by similar reasoning TZ also belongs to a pentagon. We know that
ST belongs to a pentagon, therefore STZ is an equilateral
triangle.
Since JV belonged to a hexagon,
then SW, which is equal and parallel to SV, also belongs to a hexagon. WZ
belongs to a decagon and SWZ is a right angle, therefore SZ belongs to a
pentagon. Then by similar reasoning TZ also belongs to a pentagon. We know that
ST belongs to a pentagon, therefore STZ is an equilateral
triangle.
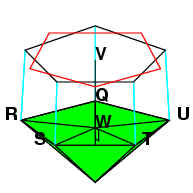 Similarly, the triangles TVZ, UQZ, QRZ and RSZ are equilateral.
Similarly, the triangles TVZ, UQZ, QRZ and RSZ are equilateral.
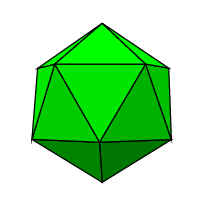 Therefore an icosahedron has been constructed, and it is contained by twenty
equilateral triangles.
Therefore an icosahedron has been constructed, and it is contained by twenty
equilateral triangles.
Proof that an Icosohedron is a Regular Polyhedron
To prove that the icosahedron is a regular polyhedron, we need to show that the figure satisfies four conditions:
a) All of its faces are regular polygons.
b) All the faces are congruent
c) The figure is convex.
d) All of its vertices are congruent.
By construction by Euclid’s proof, we know that the icosahedron is constructed of 20 equalateral triangles. Therefore all of its faces are all the same equilateral triangle, and condition (a) and (b) are satisfied.
We recognize a convex polyhedron by the fact that any segments which join two vertices not joined by an edge, the diagonals of the polyhedron, are all inside the figure.
By definition, a set in Euclidean space is convex if it contains all the line segments connecting any pair of its points. From a given point, all the diagonals from that point of the icosahedron are drawn, and shown to be inside the solid, and therefore (c) is satisfied.

We show that all the vertices are congruent by showing that the same number of faces around each vertex is the same for all vertices.
Let A be the interior angle of a face at a vertex. All of these angles are equal since we have already shown that each face is constructed with a regular polygon, and by definition all its angles are equal.
Let p be the number of edges around each face. Since each face is the same regular polygon, the number of edges is the same for each face.
Let q be the number of faces around each vertex.
We know that
A = 180 – 360/p
For example, with the icosahedron, each face is a triangle,
and therefore p=3 and A = 60o.
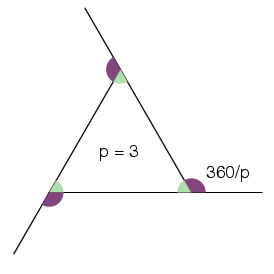
We also know that qA < 360.
For example, we look at equilateral triangles. We must have a minimum of three triangles to form a solid, since two will only form a flat plane. The total angle with three triangles is 180o (3 x 60o), and this is the vertex of a tetrahedron. Four triangles gives 240o, which is the vertex of an octahedron, five triangles gives 300 o , the vertex of an icosahedron. However, since an equilateral triangle ia two-thirds of a right angle, six triangles gives 360 o and is flat. Therefore six triangles cannot form an angle of a solid because they must all be planar.
In a similar manner, we can show that for squares and pentagons that qA is less than 360o.
We also know that p>2 and q>2, since each face must have at least 3 sides, and at least 3 faces must meet at each vertex.
Then using these facts we can construct a table
|
p = 3 |
A = 60 |
60q < 360, q < 6 |
q = 3,4,5 |
p = 3 |
|
p = 4 |
A = 90 |
90q < 360, q < 4 |
q = 3 |
p = 4 |
|
p = 5 |
A = 108 |
108q < 360, q < 10/3 |
q = 3 |
p = 5 |
|
p = 6 |
A = 120 |
120q < 360, q < 3 |
no q |
p = 6 |
Therefore there are only five possibilities
For:
p = 3, q = 3, the polyhedron is a tetrahedron, a four faced figure, for which 3 equilateral triangles meet at each vertex
p = 3 q = 4, the polyhedron is an octahedron, an eight faced figure for which 4 equilateral triangles meet at each vertex.
p = 3, q = 5, the polyhedron is a icosahedron, a twenty faced figure for which 5 equilateral triangles meet at each vertex.
p =4, q = 3 the polyhedron is a cube, an eight faced figure for which 3 squares meet at each vertex.
p = 5, q = 3, the polygon is a dodecagon, a twelve faced figure for which 3 pentagons meet at each vertex.
Therefore there are only five such combinations, and therefore there are only 5 regular polyhedra.
Since {3, 5} is the description of the icosahedron, we know that the solid consists of faces which have 3 sides, and therefore are triangles, and that 5 triangles meet each other at the vertex. Therefore at every vertex, 5 equilateral triangles meet, and therefore every vertice is the same.
Proof by Euler’s
Theorem
Euler’s formula gives a prescribed ratio of face, edges and vertices for a polyhedron. It is:
F – E + V = 2
For F = number of faces
E = number of edges
V = number of vertices
Proof that there are
only five regular convex polyhedra
Let a convex polyhedron have p edges on each face. Then there are a total number of pF edges. But since edge is shared by 2 faces, then there is only half of this number, or pF = 2E. Let q be the number of edges that meet at every vertex. Since two vertices are connected by an edge, qV = 2E.
We substitute F = 2E/p and V = 2E/q into Euler’s formula:
F – E + V = 2
2E/p – E + 2E/q = 2
1/p + 1/q = ½ + 1/E
We know that p![]() 3 and
q
3 and
q![]() 3,
because a polygon cannot have less than 3 vertices and 3 sides. Both p and q
cannot be simultaneously larger than 3,
3,
because a polygon cannot have less than 3 vertices and 3 sides. Both p and q
cannot be simultaneously larger than 3,
1/p + 1/q > ¼ + ¼ = ½ < ½
+1/E
since the number of edges cannot be 0.
Therefore p = 3 or q = 3.
If we let p = 3
1/3 + 1/q = ½ + 1/E
1/q – 1/6 = 1/E
Letting q = 3
1/3 + 1/3 = ½ + 1/E
gives E = 6
Letting q = 4
1/3 +1/4 = ½ + 1/E
give E = 12
Letting q = 5
1/3 +1/5 = ½ + 1/E
gives E= 30.
We show that q cannot equal 6 by
1/3 +1/6 = ½ + 1/E
and E = 0, which is not possible.
Similarly, we can let q = 3, then we find that p can be 3, 4 or 5.
These 5 combinations represent the 5 regular polyhedra:
For {p,q}
{3, 3} is a tetrahedron. Four faced figure, for which 3 equilateral triangles meet at each vertex
{3, 4} is an octahedron. Eight faced figure for which 4 equilateral triangles meet at each vertex.
{3, 5} is a icosahedron. Twenty faced figure for which 5 equilateral triangles meet at each vertex.
{4, 3}is a cube. Eight faced figure for which 3 squares meet at each vertex.
(5, 3) is a dodecagon. Twelve faced figure for which 3 pentagons meet at each vertex.
Therefore there are only five such combinations, and therefore there are only 5 regular polyhedra.
Since {3, 5} is the description of the icosahedron, we know that the solid consists of faces which have 3 sides, and therefore are triangles, and that 5 triangles meet each other at the vertex. Therefore at every vertex, 5 equilateral triangles meet, and therefore every vertice is the same.
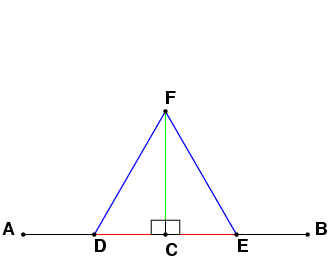
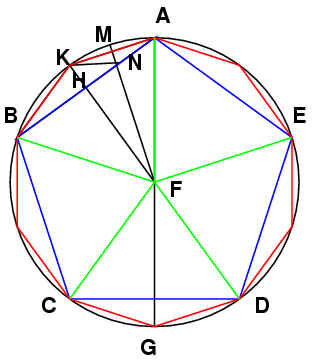
Take the 5 sided pyramid shape constructed by five equilateral triangular faces of an icoshedron which join together at one vertex. Each side is an equilateral triangle and the base is a pentagon. The five vertices of the pentagon are ABCDE, with the top of the pyramid, X. We are looking for the angle between the face ABX and the face AXE.
Let F be the midpoint between A and X. Then the angle BFE is the angle between the two faces ABX and AXE.
BF and FE are the altitudes of the faces ABX and AZE, and
they have the length![]() . Using trigonometry, the line BE is equal to
2·sin(54°).
. Using trigonometry, the line BE is equal to
2·sin(54°).
 The symmetry of a figure is any strict transformation that takes the figure into itself.
The symmetry of a figure is any strict transformation that takes the figure into itself.
 The equilateral triangle has 3-fold symmetry, this means that it can be rotated into itself through 360/3 degrees.
The equilateral triangle has 3-fold symmetry, this means that it can be rotated into itself through 360/3 degrees.  The axis of symmetry is a line that can but cut to divide the object and make 2 pieces that are mirror of each other.
The axis of symmetry is a line that can but cut to divide the object and make 2 pieces that are mirror of each other.
 The equilateral triangle has three axes of symmetry.
The equilateral triangle has three axes of symmetry.
 Since the equilateral triangle has 6 symmetry transformations, it can be divided into 6 triangles, all congruent to each other. These triangles are referred to as the symmetry chambers of the figure.
Since the equilateral triangle has 6 symmetry transformations, it can be divided into 6 triangles, all congruent to each other. These triangles are referred to as the symmetry chambers of the figure.
 Fix a chamber on a face of the equilateral triangle.
Fix a chamber on a face of the equilateral triangle.
 The chamber can be reflected through to the adjacent chamber by a matrix operation.
The chamber can be reflected through to the adjacent chamber by a matrix operation.
 Fix a chamber on a face of the regular icosahedron. Make the chamber 3D by extending its vertices to the origin, O.
Fix a chamber on a face of the regular icosahedron. Make the chamber 3D by extending its vertices to the origin, O.
 Fix s1 at (1,0,0). Assume s2 is in the x, y paln eand that y >0,also that s3 is in th region eith z>0;
Fix s1 at (1,0,0). Assume s2 is in the x, y paln eand that y >0,also that s3 is in th region eith z>0;
References:
Avnet, Jeremy and Chisholm, Matt. Finding Face-to-Face Angles.
[Theory.org]
Bogomolny, Alexander. Interactive Mathematics Miscellany and Puzzles.
[Cut The Knot]
Bourke, Paul. Platonic Solids (Regular polytopes in 3D).
[Platonic Solids]
Casselman, Dr. W.. A Manual of
Mathematical Illustration. [MATH 308
text]
Casselman, Dr. W..
Geometrical Symmetry and the Fine Structure of Regular Polyhedra.
[Notes on
Symmetry]
Joyce, David E..
Euclids Elements.
[Euclid]
MacLean, Kenneth J. M.. The Icosahedron.
[Geometry Web Page]
To run PostScript files
a PostScript interpreter is needed.
These can be found at: http://www.cs.wisc.edu/~ghost