Given a non-negative integer $m$, let $\Omega_m$ denote the set of vectors $\omega = (\omega_1, \dots, \omega_m) \in [0, 1]^m$ such that $\sum_i{\omega_i} = 1$. The set $\Omega_m$ is together with a metric $d_M$, that is the Manhattan distance between vectors, i.e., $\forall \omega, \omega' \in \Omega_m$, $d_M(\omega, \omega') = \sum_i{|\omega_i - \omega'_i|}$. Given $S \subseteq \Omega_m$, we denote $\min(d_M, S) = \min_{\omega, \omega' \in S}{d_M(\omega, \omega')}$.This is essentially a packing problem. In the case $m=3$, I have used SMT solvers (MathSAT 5 and Z3) to compute optimal solutions up to $k=19$ (by this point the program is getting quite slow, so I don't think we can go much farther than that by this method). The basic idea is the following. We have $2k$ variables $x_i, y_i$, $i = 1 \ldots k$. To cut down degeneracy a bit, we may assume $x_i \le x_{i+1}$ for $1 \le i < k$. Moreover, we can assume if $x_i = x_{i+1}$ then $y_i < y_{i+1}$. If we want distance $\ge r$ between all vectors, we have constraints of the form $$ |x_i - x_j| + |y_i - y_j| + |x_i + y_i - x_j - y_j| \ge r $$ for $1 \le i < j \le k$, which can be written as $$ (x_j - x_i) + (y_i - y_j) + (x_i + y_i - x_j - y_j) \ge r \ {\bf or} \ (x_j - x_i) + (y_i - y_j) - (x_i + y_i - x_j - y_j) \ge r \ {\bf or} \\ (x_j - x_i) - (y_i - y_j) + (x_i + y_i - x_j - y_j) \ge r \ {\bf or} \ (x_j - x_i) - (y_i - y_j) - (x_i + y_i - x_j - y_j) \ge r $$ I give the set of constraints to the SMT solver and ask it whether they can be satisfied, and if so to find a solution. If they can be satisfied, we can then ask if it is possible to do better. For this it's convenient to make $r$ a variable. Initially we have the constraint $r \ge r_0$ where $r_0$ is our initial guess at the best possible distance. If it is possible, we try adding the additional constraint $r > r_0$. If the solver answers "sat", i.e. it is possible, with $r \ge r_0$ but "unsat", i.e. it is not possible, with $r > r_0$, then we know we have the optimal $r_0$. If $r \ge r_0$ is "unsat" we can reduce $r_0$ and try again, while if $r > r_0$ is "sat" we can increase $r_0$ and try again. Here are examples for $k=8$ of the SMT input file and output.I am interested in the following ``most diverse $k$-subset'' problem: given two non-negative integers $m, k$, return a set $S \subset \Omega_m$ of size $k$ that maximizes $\min(d_M, S)$ (i.e., $S$ is such that $\forall S' \subset \Omega_m$ with $|S'| = k$, we have $\min(d_M, S') \leq \min(d_M, S)$).
For example, if $m = 3$ and $k = 4$, it seems that the only possible resulting set is $S = \{(0, 0, 1), (0, 1, 0), (1, 0, 0), (1/3, 1/3, 1/3)\}$, with $\min(d_M, S) = 4/3$.
What would be the general algorithm to compute $S$, for all non-negative integers $m, k$?
This problem is nice in that the constraints only involve piecewise-linear inequalities with integer coefficients, so we can be sure that the optimal solution will involve rational numbers (hopefully with small denominators). It usually took at most a few tries to find an optimal solution. Things did slow down, however, as $k$ increased: for $k=16$ with the optimal $r_0$, the computation on MathSAT took over 21 hours.
Here are the optimal solutions my program found for $k$ from $2$ to $19$:
$k = 2$: [[0, 0, 1], [1/4, 3/4, 0]]

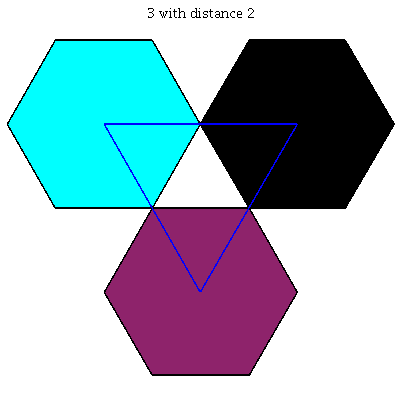
$k = 3$: [[0, 0, 1], [0, 1, 0], [1, 0, 0]]
$k = 4$: [[0, 0, 1], [0, 1, 0], [1/3, 1/3, 1/3], [1, 0, 0]]

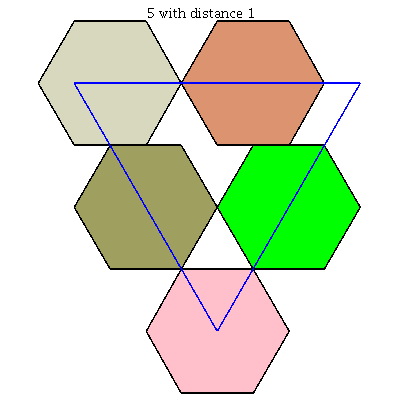
$k = 5$: [[0, 0, 1], [0, 1/2, 1/2], [1/8, 7/8, 0], [1/2, 0, 1/2], [5/8, 3/8, 0]]
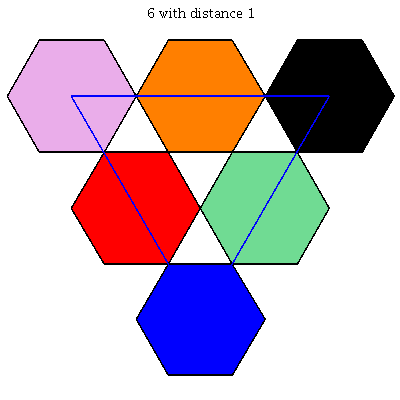
$k = 6$: [[0, 0, 1], [0, 1/2, 1/2], [0, 1, 0], [1/2, 0, 1/2], [1/2, 1/2, 0], [1, 0, 0]]
$k = 7$: [[0, 0, 1], [0, 23/40, 17/40], [0, 1, 0], [3/8, 1/40, 3/5], [3/8, 3/5, 1/40], [3/5, 1/5, 1/5], [1, 0, 0]]
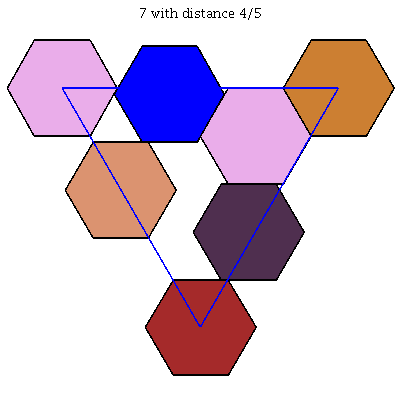
$k = 8$: [[0, 0, 1], [0, 3/8, 5/8], [0, 1, 0], [1/8, 5/8, 1/4], [3/8, 0, 5/8], [1/2, 1/2, 0], [5/8, 1/8, 1/4], [1, 0, 0]]
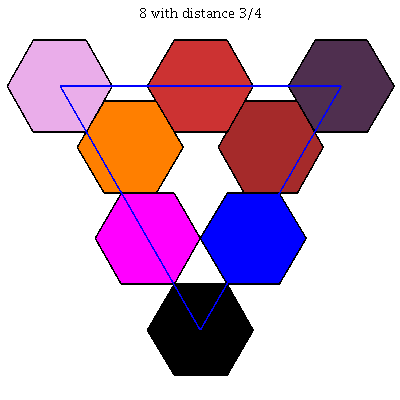
$k = 9$: [[0, 0, 1], [0, 19/30, 11/30], [1/30, 3/10, 2/3], [1/30, 14/15, 1/30], [1/3, 1/3, 1/3], [11/30, 0, 19/30], [11/30, 19/30, 0], [2/3, 1/30, 3/10], [1, 0, 0]]
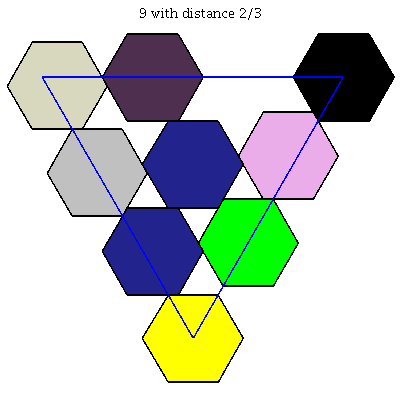
$k = 10$: [[0, 0, 1], [0, 1/3, 2/3], [0, 2/3, 1/3], [0, 1, 0], [1/3, 0, 2/3], [1/3, 1/3, 1/3], [1/3, 2/3, 0], [2/3, 0, 1/3], [2/3, 1/3, 0], [1, 0, 0]]
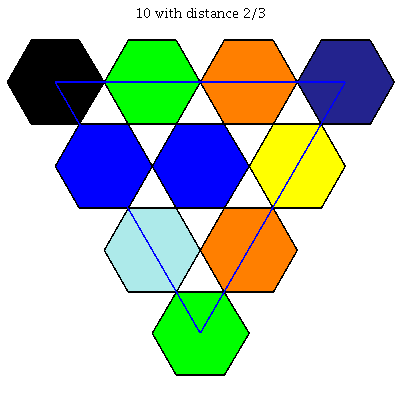
$k = 11$: [[0, 0, 1], [0, 7/20, 13/20], [0, 1, 0], [1/80, 51/80, 7/20], [1/4, 1/20, 7/10], [1/4, 7/10, 1/20], [5/16, 27/80, 7/20], [11/20, 0, 9/20], [11/20, 9/20, 0], [7/10, 3/20, 3/20], [1, 0, 0]]
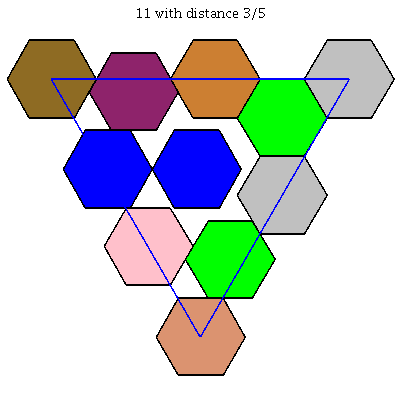
$k = 12$: [[0, 0, 1], [0, 2/7, 5/7], [0, 5/7, 2/7], [0, 1, 0], [1/7, 3/7, 3/7], [2/7, 0, 5/7], [2/7, 5/7, 0], [3/7, 1/7, 3/7], [3/7, 3/7, 1/7], [5/7, 0, 2/7], [5/7, 2/7, 0], [1, 0, 0]]
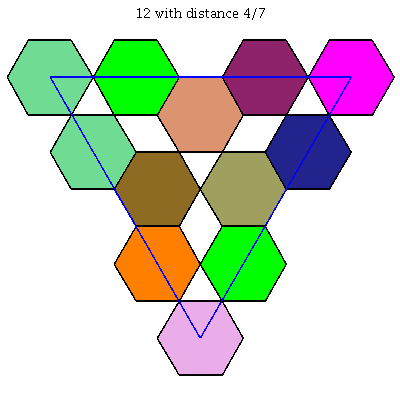
$k = 13$: [[0, 0, 1], [0, 1/3, 2/3], [0, 3/5, 2/5], [0, 1, 0], [2/15, 11/15, 2/15], [1/5, 1/15, 11/15], [4/15, 4/15, 7/15], [2/5, 3/5, 0], [7/15, 0, 8/15], [7/15, 1/3, 1/5], [43/60, 1/60, 4/15], [11/15, 4/15, 0], [59/60, 0, 1/60]]

$k = 14$: [[0, 0, 1], [0, 1/4, 3/4], [0, 1/2, 1/2], [0, 1, 0], [5/24, 13/24, 1/4], [1/4, 0, 3/4], [1/4, 7/24, 11/24], [1/4, 3/4, 0], [11/24, 1/24, 1/2], [23/48, 1/2, 1/48], [1/2, 1/4, 1/4], [35/48, 0, 13/48], [3/4, 1/4, 0], [1, 0, 0]]
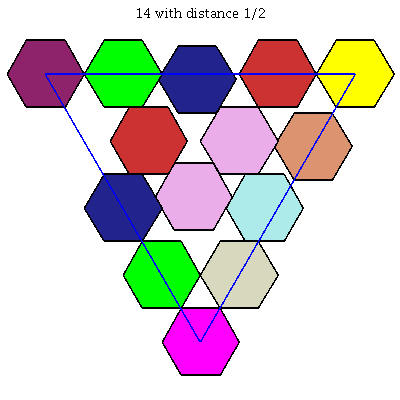
$k = 15$: [[0, 1/80, 79/80], [0, 1/2, 1/2], [0, 1, 0], [1/40, 1/4, 29/40], [9/80, 51/80, 1/4], [1/4, 0, 3/4], [1/4, 31/80, 29/80], [1/4, 3/4, 0], [29/80, 11/80, 1/2], [31/80, 1/2, 9/80], [1/2, 1/4, 1/4], [49/80, 0, 31/80], [51/80, 29/80, 0], [3/4, 9/80, 11/80], [1, 0, 0]]
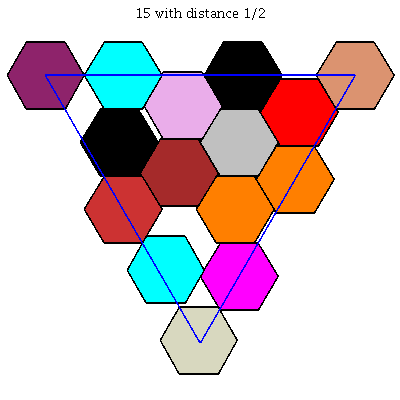
$k = 16$: [[0, 0, 1], [0, 1/3, 2/3], [0, 16/21, 5/21], [0, 1, 0], [1/21, 11/21, 3/7], [1/7, 2/21, 16/21], [5/21, 5/21, 11/21], [5/21, 16/21, 0], [2/7, 3/7, 2/7], [8/21, 0, 13/21], [3/7, 11/21, 1/21], [11/21, 5/21, 5/21], [13/21, 0, 8/21], [2/3, 1/3, 0], [16/21, 2/21, 1/7], [1, 0, 0]]
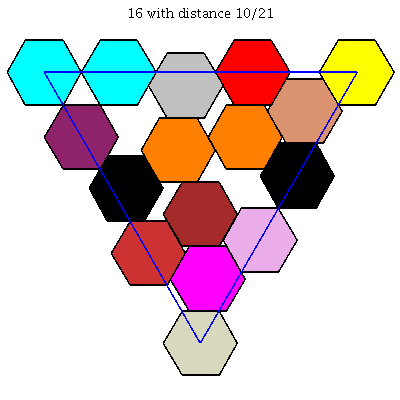
$k = 17$: [[0, 0, 1], [0, 4/13, 9/13], [0, 9/13, 4/13], [0, 1, 0], [1/13, 6/13, 6/13], [2/13, 1/13, 10/13], [2/13, 10/13, 1/13], [3/13, 3/13, 7/13], [3/13, 7/13, 3/13], [5/13, 0, 8/13], [5/13, 4/13, 4/13], [5/13, 8/13, 0], [7/13, 1/13, 5/13], [7/13, 5/13, 1/13], [10/13, 0, 3/13], [10/13, 3/13, 0], [1, 0, 0]]

$k = 18$: [[0, 2/9, 7/9], [0, 5/9, 4/9], [0, 53/54, 1/54], [1/54, 41/54, 2/9], [1/27, 0, 26/27], [1/9, 1/3, 5/9], [2/9, 1/9, 2/3], [2/9, 4/9, 1/3], [2/9, 7/9, 0], [1/3, 2/9, 4/9], [1/3, 5/9, 1/9], [4/9, 0, 5/9], [4/9, 1/3, 2/9], [5/9, 1/9, 1/3], [5/9, 4/9, 0], [7/9, 0, 2/9], [7/9, 2/9, 0], [1, 0, 0]]
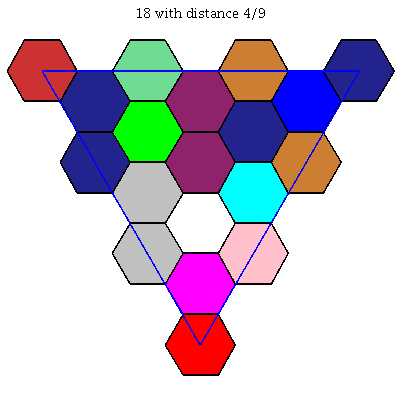
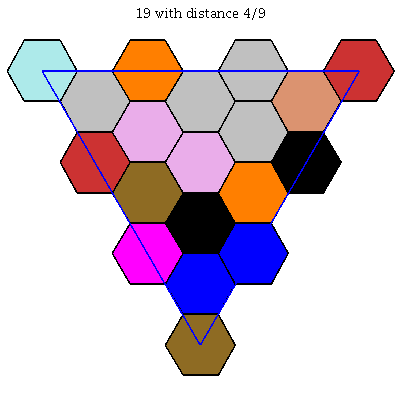
This optimal packing for $k=18$ has room in it for an extra tile of the same size, so filling that hole gives an optimal solution for $k=19$.
$k = 19$: [[0, 2/3, 1/3], [0, 0, 1], [0, 1, 0], [0, 1/3, 2/3], [1/9, 4/9, 4/9], [1/9, 7/9, 1/9], [1/9, 1/9, 7/9], [2/9, 5/9, 2/9], [1/3, 1/3, 1/3], [1/3, 0, 2/3], [1/3, 2/3, 0], [4/9, 1/9, 4/9], [4/9, 4/9, 1/9], [5/9, 2/9, 2/9], [2/3, 0, 1/3], [2/3, 1/3, 0], [7/9, 1/9, 1/9], [1, 0, 0], [2/9, 2/9, 5/9]]