Method of Undetermined Coefficients

The method of undetermined coefficients is an example of a common theme in mathematics: to solve a problem, first decide on the general form a solution should have (containing some unknown coefficients), then see what the coefficients must be in order to have a solution. The trick is to be able to guess the general form. In this section, we will use this method on constant-coefficient equations of the form $(D^2 + p D + q) y = g(x)$ where $g(x)$ is a sum of terms which can be a polynomial, possibly times an exponential, possibly times a sine or cosine.

First we consider polynomials $g(x)$. The rule will be the following:

Let $g(x)$ be a polynomial of degree $n$, and $P(D) = D^2 + pD + q$.

• If $q \ne 0$, $P(D) y = g(x)$ has a solution that is a polynomial of the same degree $n$.
• If $q = 0$ but $p \ne 0$, it has a solution that is a polynomial of degree $n+1$ with no constant term.
• If $p = q = 0$, it has a solution that is a polynomial of degree $n+2$ with no constant term and no $x$ term.

Example: Find a solution of $(D^2 - D + 4) y = 4 x^2 - 1$.

The rule tells us to consider a polynomial of degree 2, $y = A_2 x^2 + A_1 x + A_0$. Plugging this into the equation, we get

$$4 A_2 x^2 + (- 2 A_2 + 4 A_1) x + (2 A_2 - A_1 + 4 A_0) = 4 x^2 - 1$$

In order for this to be true (as an equation of two functions, not just for some particular $x$), the coefficients of each power of $x$ must match on both sides. We must have $4 A_2 = 4$, $- 2 A_2 + 4 A_1 = 0$, $2 A_2 - A_1 + 4 A_0 = -1$. This is easy to solve, first for $A_2$, then $A_1$, then $A_0$. We get $A_2 = 1$, $A_1 = 1/2$, $A_0 = -5/8$. Thus our solution is $y = x^2 + x/2 - 5/8$.

Example: Find a solution of $(D^2 - D) y = 6 x^2 - 1$.

This time we take $y = A_3 x^3 + A_2 x^2 + A_1 x$, and get

$$- 3 A_3 x^2 + (6 A_3 -2 A_2) x +(2 A_2 - A_1) = 6 x^2 - 1$$

Again solving three equations (one from each coefficient), we get the solution $y = -2 x^3 - 6 x^2 - 11 x$.

Example: Find a solution of $D^2 y = 20 x^3 - 2 x$.

For this one we don't need anything fancy: just integrate twice. A solution is $y = x^5 - x^3/3$.

Now, how do we know this will always work? After all, a system of equations doesn't always have solutions. One way to see it is the following. First consider the first-order equation $(D+a) y = g(x)$, where $a \ne 0$ and $g(x)$ is a polynomial of degree $n$. We have a formula for the solution of a first order linear equation:

$$\mu(x) = \exp \int a dx = \exp(a x)$$

$$y = \mu(x)^{-1} \left(\int \mu(x) g(x) dx + C\right) = \exp(-a x) \left(\int \exp(a x) g(x) dx + C \right)$$

Using integration by parts, one antiderivative is $\exp(a x)$ times a polynomial of degree $n$, and the corresponding $y$ is a polynomial of degree $n$.

For example, for $(D+2) y = x^2 + 1$, we have

$$\vcenter{\openup.7ex\mathsurround=0pt \ialign{\strut\hfil... ...) - \frac{x}{2} \exp(2 x) + \frac{1}{4} \exp(2 x) \cr\crcr}}$$

and the polynomial solution is $y = x^2/2 - x/2 + 3/4$.

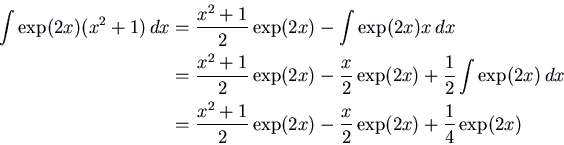
Now consider our second-order equation $(D^2 + p D + q) y = g(x)$. We can write $D^2 + p D + q = (D + a)(D + b)$ for some (not necessarily real) constants $a$ and $b$.

• If $q \ne 0$, $a \ne 0$ and $b \ne 0$. There is a polynomial $u(x)$ of degree $n$ with $(D+a) u = g(x)$, and then a polynomial $y(x)$ of degree $n$ with $(D+b) y = u(x)$. Thus $(D+a)(D+b)y = (D+a)u = g(x)$.
• If $q = 0$ but $p \ne 0$, $D^2 + p D = (D + p) D$. There is a polynomial $u(x)$ of degree $n$ with $(D+p) u = g(x)$. Integrating $u(x)$, we get $y(x)$ of degree $n+1$ with no constant term such that $D y = u(x)$ and $(D+p) D y = (D+p) u = g(x)$.
• If $q = 0$ and $p = 0$, we just integrate $g(x)$ twice, to obtain $y(x)$ of degree $n+2$ with no constant or $x$ term.

Now suppose $g(x)$ is a polynomial times an exponential. The simplest way is to use the Exponential Shift Theorem.

Example: Find a solution of $(D^2 - D + 4) y = (x^2 - x) \exp(2 x)$.

If $y = u(x) \exp(2 x)$ we have

$$\vcenter{\openup.7ex\mathsurround=0pt \ialign{\strut\hfil... ...2 - x) \exp(2 x)\cr (D^2 + 3 D + 6) u &= x^2 - x \cr\crcr}}$$

This puts us back in the polynomial case. We should have a solution where $u$ is a polynomial of degree 2, and thus $y$ is a polynomial of degree 2 times $\exp(2 x)$. Namely, using the methods we looked at before, $u(x) = x^2/6 - x/3 + 1/9$.

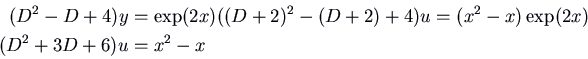
What happens in general? Suppose we want a solution of $P(D) y = f(x) \exp(a x)$, where $f(x)$ is a polynomial of degree $n$. Using the Exponential Shift Theorem, we look for a solution $y = u(x) \exp(a x)$ where $P(D+a) u = f(x)$. Now:

• If $a$ not a root of $P$, i.e. $P(D) = (D-b)(D-c)$ where neither $b$ nor $c$ is $a$, then $P(D+a) = (D+a-b)(D+a-c)$ has a nonzero constant term, so we get a polynomial $u(x)$ of degree $n$.
• If $a$ is one of two roots of $P$, i.e. $P(D) = (D-b)(D-a)$ with $b \ne a$, then $P(D+a) = (D+a-b)D$, and we get $u(x)$ of degree $n+1$ with no constant term.
• If $a$ is a double root of $P$, i.e. $P(D) = (D-a)^2$, then $P(D+a) = D^2$ and we get $u(x)$ of degree $n+2$ with no constant or $x$ term.

Example: Find a solution of $(D^2 + D - 6) y = (15 x^2 - 4 x - 12) \exp(2 x)$.

We have $P(D+2) = (D+2)^2 + (D+2) - 6 = D^2 + 5 D$. With $u(x) = A_3 x^3 + A_2 x^2 + A_1 x$ we'll have $(D^2 + 5 D) u = 15 x^2 - 4 x - 12$. The left side is $15 A_3 x^2 + (10 A_2 + 6 A_3) x + (5 A_1 + 2 A_2)$. Solving the equations, we get $A_3 = 1$, $A_2 = -1$, $A_1 = -2$. So our solution is $y = (x^3 - x^2 - 2 x) \exp(2 x)$.

If $g(x) = f(x) \exp(a x) \sin(b x)$ or $f(x) \exp(a x) \cos(b x)$, we can deal with it similarly using the complex exponential $\exp((a+bi)x)$. If $a+bi$ is not a root of $P$, the polynomial will have the same degree as $f$. If it is a root, the polynomial will have one degree higher and no constant term. It won't be a double root because complex roots come in pairs.

Example: Find a solution of $(D^2 + D - 1) y = x \cos x$.

We have $\cos x = {\rm Re }\exp(i x)$, so we will solve $(D^2 + D - 1) z = x \exp(i x)$ and take $y = {\rm Re }z$. We have $(D+i)^2 + (D+i) - 1 = D^2 + (1+2i) D -2 + i$. We will have $z = u(x) \exp(i x)$ with $u(x) = A_1 x + A_0$. Now $(D^2 + (1+2i) D -2 + i) u(x) = (-2+i) A_1 x + (1+2i) A_1 + (-2+i) A_0$. Solving our equations $(-2+i) A_1 = 1$ and $(1+2i) A_1 + (-2+i) A_0 = 0$, we get $A_1 = (-2-i)/5$ and $A_0 = (1-2i)/5$. So $z = ((-2-i) x/5 + (1-2i)/5) \exp(i x)$ and $y = {\rm Re }z = (-2 x \cos x + x \sin x + \cos x + 2 \sin x)/5$.

If you don't like all the complex arithmetic, you can use the method of undetermined coefficients directly on the real form: in this case it will be $y = (A_1 x + A_0) \cos x + (B_1 x + B_0) \sin x$. Then we have $(D^2+D-1)y = (-2 A_1 + B_1) x \cos x + (-2 A_0 + A_1 + B_0 + 2 B_1) \cos x + (-A_1 - 2 B_1) x \sin x + (-A_0 - 2 A_1 - 2 B_0 + B_1) \sin x$. For this to be $x \cos x$, we need the four equations $-2 A_1 + B_1 = 1$, $-2 A_0 + A_1 + B_0 + 2 B_1=0$, $-A_1 - 2 B_1 = 0$, $-A_0 - 2 A_1 - 2 B_0 + B_1 = 0$.