Separable Equations

A differential equation is separable if it can be written with one variable only on the left and the other variable only on the right:

f(y) y' = g(x)

or, writing y' = dy/dx and formally multiplying by dx:

$$f(y)\, dy = g(x)\, dx$$

We can then integrate both sides:

$$\int f(y)\, dy = \int g(x)\, dx + C$$

The result is generally an implicit equation involving a function of x and a function of y. It may or may not be possible to solve this to get y explicitly as a function of x. For an initial value problem, substitute the values of x and y to get the value of C.

Example:

$$\frac{dy}{dx} = (x-1) y^2, \ \ y(0) = 3$$

We put the y factors on the left, the x factors on the right, and integrate:

$$\displaylines{ \int \frac{1}{y^2} \, dy = \int (x-1) \, dx + C \cr - \frac{1}{y} = \frac{x^2}{2} - x + C \cr}$$

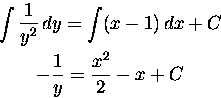
Substituting x=0, y=3 we have C = -1/3. Then solving for y,

$$y = \frac{6}{-3 x^2 + 6 x + 2}$$

But is this defined for all x? Not if the denominator is ever 0. As it happens, the denominator is 0 for two values of x. Since our initial condition is at x = 0, the solution is defined on an interval containing 0:

$$1 - \frac{\sqrt{15}}{3} < x < 1 + \frac{\sqrt{15}}{3}$$

Here is the graph of the solution, together with the direction field:

This illustrates an important point: a solution of a differential equation may ``blow up'' as the independent variable approaches a certain finite value, from the left or from the right, having a vertical asymptote. Thus the solution may only be defined on an interval, rather than on the whole real line. Even though the formula for the solution is also defined on the other side of the vertical asymptote, we don't consider that as part of the solution.