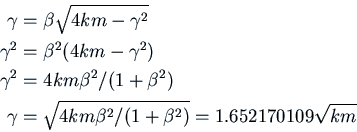Designing a Measuring Instrument
 A measuring instrument typically shows its value using a needle that
swings across a scale. In some cases the needle may oscillate
about the correct reading, and it may be some time until it settles
down enough for an accurate
reading to be made. On a typical bathroom scale, for example,
this may take several seconds. In cases where speed and accuracy
are important, such a delay may be unacceptable, and instruments
should be designed to produce an accurate reading as quickly as
possible.
A measuring instrument typically shows its value using a needle that
swings across a scale. In some cases the needle may oscillate
about the correct reading, and it may be some time until it settles
down enough for an accurate
reading to be made. On a typical bathroom scale, for example,
this may take several seconds. In cases where speed and accuracy
are important, such a delay may be unacceptable, and instruments
should be designed to produce an accurate reading as quickly as
possible.
We will model the measuring instrument as a mass on a spring.
The equilibrium position represents the quantity to be measured.
The
mass 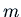 and spring constant
and spring constant 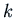 are given, but the damping constant
are given, but the damping constant
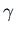 is under our control. The system will start at some value
is under our control. The system will start at some value
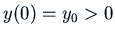 with
with 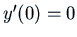 , and at some time we will take the
measurement
, and at some time we will take the
measurement 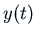 . We want to be sure that
. We want to be sure that 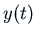 is within
is within
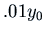 of the equilibrium value 0.
of the equilibrium value 0.
In order to ensure this,
we should wait until some time 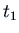 , long enough that
, long enough that
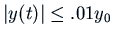 for all
for all 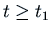 . It is not good enough just
to have
. It is not good enough just
to have
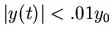 at some time
at some time 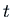 if this is not always
true later, because it would be hard to ensure that the measurement
is taken at the right time. We want to choose
if this is not always
true later, because it would be hard to ensure that the measurement
is taken at the right time. We want to choose 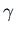 to
minimize
to
minimize 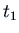 .
.
I claim that the best 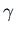 is for an underdamped system where the first
minimum of
is for an underdamped system where the first
minimum of 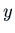 is at
is at 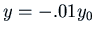 . We'll find the
. We'll find the 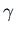 value that
satisfies this, and then justify the claim.
value that
satisfies this, and then justify the claim.
Recall that the general solution for free underdamped vibration is of the form
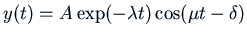 . The quasi-period is
. The quasi-period is
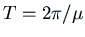 . Note that
. Note that
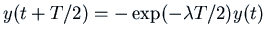 .
Thus if
.
Thus if 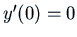 (the first maximum is at
(the first maximum is at 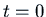 ), the first minimum
occurs at
), the first minimum
occurs at 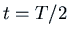 . The value of
. The value of 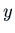 at this first minimum is
at this first minimum is
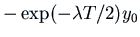 . So we want
. So we want
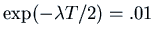 , i.e.
, i.e.
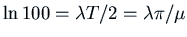 . Let
. Let
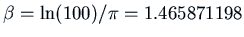 . We want
. We want
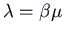 .
Since
.
Since
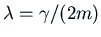 and
and
 we have
we have
This is to be compared with
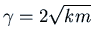 which would correspond to
critical damping.
which would correspond to
critical damping.
With this value of 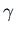 , we have
, we have
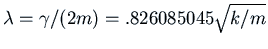 and
and
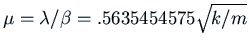 .
Then
.
Then
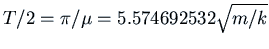 . The reading can
be taken some time before this, although the precise time is not
so easy to determine. However, as a practical matter we might
wait until the first minimum to take the reading, since the first
minimum is easy to see by eye.
. The reading can
be taken some time before this, although the precise time is not
so easy to determine. However, as a practical matter we might
wait until the first minimum to take the reading, since the first
minimum is easy to see by eye.
With
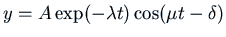 , we have
, we have
We want 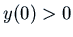 so
so
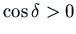 . Thus
. Thus
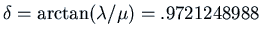 . Then since
. Then since
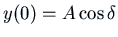 we get
we get
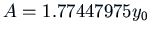 .
Now we want to solve
.
Now we want to solve
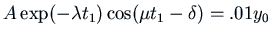 .
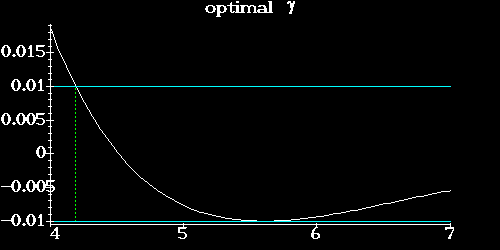
Numerical methods indicate
.
Numerical methods indicate
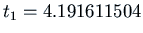 .
.
Now let's see why this  makes
makes 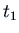 a minimum. If we decrease
a minimum. If we decrease 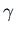 slightly,
the first minimum is below
slightly,
the first minimum is below 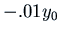 , and we would have to wait until
some time after
, and we would have to wait until
some time after 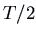 before taking the measurement. On the other hand,
if we increase
before taking the measurement. On the other hand,
if we increase 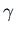 it will take longer to reach
it will take longer to reach 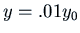 .
So our
.
So our 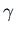 should indeed be a minimum.
(This isn't a complete proof, but it should make the result plausible)
should indeed be a minimum.
(This isn't a complete proof, but it should make the result plausible)
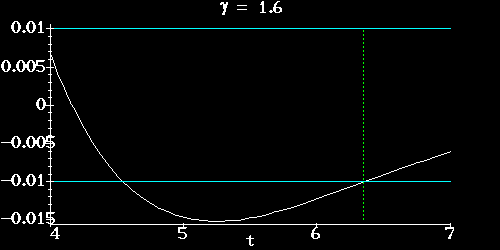
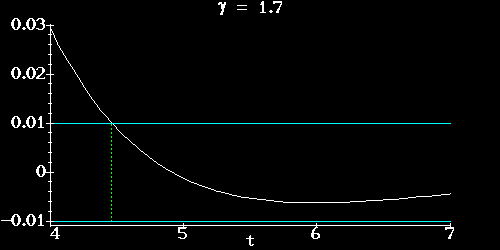
Here are the graphs of 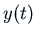 for
for 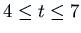 in four cases, all
with
in four cases, all
with 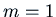 and
and 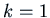 :
our value
:
our value
 ,
, 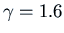 ,
, 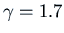 , and the critical
damping case
, and the critical
damping case 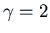 .
.

Robert Israel
2002-02-18
 A measuring instrument typically shows its value using a needle that
swings across a scale. In some cases the needle may oscillate
about the correct reading, and it may be some time until it settles
down enough for an accurate
reading to be made. On a typical bathroom scale, for example,
this may take several seconds. In cases where speed and accuracy
are important, such a delay may be unacceptable, and instruments
should be designed to produce an accurate reading as quickly as
possible.
A measuring instrument typically shows its value using a needle that
swings across a scale. In some cases the needle may oscillate
about the correct reading, and it may be some time until it settles
down enough for an accurate
reading to be made. On a typical bathroom scale, for example,
this may take several seconds. In cases where speed and accuracy
are important, such a delay may be unacceptable, and instruments
should be designed to produce an accurate reading as quickly as
possible.