Sample Questions: First Order Systems

1. Find the general solution of the following system of differential equations:
   
   $$\vcenter{\openup.7ex\mathsurround=0pt \ialign{\strut\hfi... ...& x_1 - 9 x_2 + 10\cr \frac{dx_2}{dt} =& x_1 + x_2\cr\crcr}}$$
   
   

   Solution

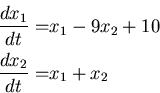
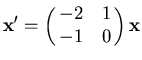2. Find all solutions of the system $${\bf x}' = \pmatrix{-2 & 1\cr -1 & 0\cr} {\bf x}$$ of the form $${\bf x}= {\rm e}^{rt} {\bf u}$$ where $r$ is a constant and ${\bf u}$ is a constant vector.

   Solution

3. Consider the nonlinear system
   
   $$\,\vcenter{\openup.7ex\mathsurround=0pt \ialign{\strut\hfil... ... \crcr dx/dt &= x^2 + y^2 - 2 \cr dy/dt &= x - y \cr\crcr}}\,$$
   
   

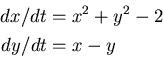
   (a) Find, classify and determine the stability of all critical points.

   (b) Indicate the direction of the direction field in various regions, and sketch the phase portrait of the system in the $xy$ plane.

   Solution

4. A spring that used to be ideal has worn out somewhat, so that the restoring force corresponding to displacement $x$ from equilibrium is now $$(k - {\rm e}^{-x^2}) x$$, where $k > 1$ is the original spring constant. Thus the equation of motion of a mass $m$ suspended from the spring is

   
   

   $$m x'' + c x' + (k - {\rm e}^{-x^2}) x = 0$$
   
   

   (a) Show that for $m=1$, $c=3$, this equation is expressible as the system
   

   $$x' = y, \quad \quad y' = - 3 y - (k - {\rm e}^{-x^2}) x \qquad (*)$$
   
   

   (b) Show that $(0,0)$ is the only critical point of the system (*), and construct its linearization about $(0,0)$.

   (c) Show that this critical point is stable.

   (d) Classify the critical point and sketch the trajectories near it when $k=3$, and also when $k=4$. Briefly contrast these two different cases in terms of the behaviour and damping of the spring-mass system near equilibrium.

   Solution

5. For the system of equations
   
   $$x' = x (-1 + y), \qquad y' = y(1 - x)$$
   
   

   (a) Find and classify all critical points.

   (b) Sketch the trajectories in the phase plane.

   (c) Find the equation of the trajectories by solving a differential equation for $dy/dx$.

   Solution