(a) For 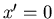 , we need
, we need 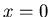 or
or 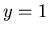 . For
. For 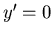 , we need
, we need 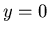 or
or 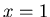 . Thus the critical points are
. Thus the critical points are 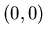 and
and 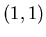 .
The Jacobian matrix is
.
The Jacobian matrix is
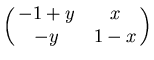 . At
. At 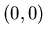 this is
this is
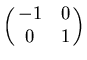 , which has eigenvalues
, which has eigenvalues 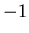 and 1.
Therefore
and 1.
Therefore 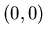 is a saddle. At
is a saddle. At 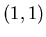 the Jacobian matrix is
the Jacobian matrix is
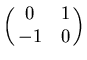 , which has eigenvalues
, which has eigenvalues 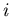 and
and 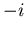 .
This is a centre in the linearization, but we don't know yet whether it
is a centre in the nonlinear system. However, we may be able to find out
by doing part (c).
.
This is a centre in the linearization, but we don't know yet whether it
is a centre in the nonlinear system. However, we may be able to find out
by doing part (c).
(c) By the Chain Rule we have
This is separable, and we can solve it:
Thus the trajectories (apart from those on 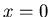 and
and 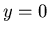 ) have implicit
equations
) have implicit
equations
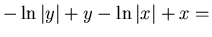 constant.
constant.
(a continued) Since the function
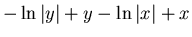 is smooth
near
is smooth
near 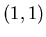 , its level curves there can be closed curves but not spirals.
So
, its level curves there can be closed curves but not spirals.
So 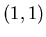 really is a centre.
really is a centre.
(b) Note that the trajectories entering and leaving the saddle 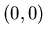 are on the
are on the 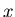 and
and 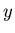 axes respectively.
axes respectively.

Robert Israel
2002-04-08
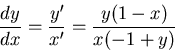
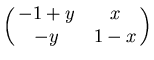 . At
. At 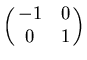 , which has eigenvalues
, which has eigenvalues 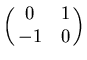 , which has eigenvalues
, which has eigenvalues 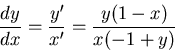
![]() is smooth
near
is smooth
near ![]() , its level curves there can be closed curves but not spirals.
So
, its level curves there can be closed curves but not spirals.
So ![]() really is a centre.
really is a centre.
![]() are on the
are on the ![]() and
and ![]() axes respectively.
axes respectively.
