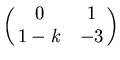 , so the linearized system is
, so the linearized system is
(b) For ![]() we need
we need ![]() , and then
, and then
![]() .
But
.
But
![]() for all
for all ![]() , so the only way to have
, so the only way to have ![]() is
is
![]() . The Jacobian matrix at
. The Jacobian matrix at ![]() is
is
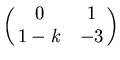 , so the linearized system is
, so the linearized system is
(c) The characteristic polynomial is
![]() , and its roots are
, and its roots are
![]() .
If the eigenvalues are real, they are both negative since
.
If the eigenvalues are real, they are both negative since
![]() . If the eigenvalues are complex, their real part is negative.
Thus in either case, the critical point is stable.
. If the eigenvalues are complex, their real part is negative.
Thus in either case, the critical point is stable.
(d) When ![]() the characteristic polynomial is
the characteristic polynomial is
![]() so the eigenvalues are
so the eigenvalues are ![]() and
and ![]() , and the critical point is a node.
The eigenvectors are
, and the critical point is a node.
The eigenvectors are
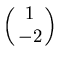 for
for ![]() (``fast'') and
(``fast'') and
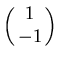 for
for ![]() (``slow'').
The trajectories are shown in the first plot below.
A solution can cross
(``slow'').
The trajectories are shown in the first plot below.
A solution can cross ![]() at most once.
This corresponds to an overdamped spring-mass system.
at most once.
This corresponds to an overdamped spring-mass system.
When ![]() the characteristic polynomial is
the characteristic polynomial is ![]() . The eigenvalues
are complex:
. The eigenvalues
are complex:
![]() . Thus the critical point is a spiral.
At
. Thus the critical point is a spiral.
At ![]() the velocity is
the velocity is
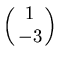 , so the direction is clockwise.
The trajectories are sketched in the second plot below. This is not an
exact plot for our system, because in the actual spiral the
distance
to the origin decreases by so much in each revolution that you could
not see a whole turn of the spiral in one picture.
Solutions will oscillate, crossing
, so the direction is clockwise.
The trajectories are sketched in the second plot below. This is not an
exact plot for our system, because in the actual spiral the
distance
to the origin decreases by so much in each revolution that you could
not see a whole turn of the spiral in one picture.
Solutions will oscillate, crossing ![]() infinitely many times.
This corresponds to an underdamped spring-mass system.
infinitely many times.
This corresponds to an underdamped spring-mass system.

