(a) For a critical point (equilibrium point) we need 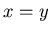 and
and
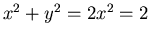 . Therefore
. Therefore 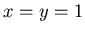 or
or 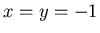 .
The Jacobian matrix is
.
The Jacobian matrix is
At the equilibrium point  the Jacobian matrix
the Jacobian matrix
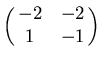 has characteristic polynomial
has characteristic polynomial
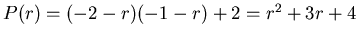 .
The eigenvalues are the roots of this, namely
.
The eigenvalues are the roots of this, namely
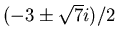 .
They are complex with negative real part, so this is a spiral attractor
(asymptotically stable spiral).
.
They are complex with negative real part, so this is a spiral attractor
(asymptotically stable spiral).
At the equilibrium point 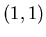 the Jacobian matrix
the Jacobian matrix
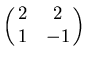 has characteristic polynomial
has characteristic polynomial
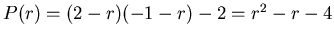 . The eigenvalues are the roots of this, namely
. The eigenvalues are the roots of this, namely
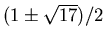 . One is positive and the other negative, so
this is a saddle point, and unstable.
. One is positive and the other negative, so
this is a saddle point, and unstable.
(b)

Robert Israel
2002-04-08
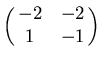 has characteristic polynomial
has characteristic polynomial
![]() the Jacobian matrix
the Jacobian matrix
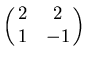 has characteristic polynomial
has characteristic polynomial
![]() . The eigenvalues are the roots of this, namely
. The eigenvalues are the roots of this, namely
![]() . One is positive and the other negative, so
this is a saddle point, and unstable.
. One is positive and the other negative, so
this is a saddle point, and unstable.
