For a particular solution,
take
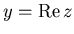 where
where
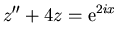 . Using Exponential Shift,
. Using Exponential Shift,
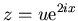 with
with
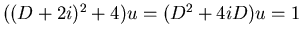 .
Taking
.
Taking 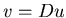 ,
, 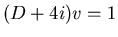 , which has a constant solution
, which has a constant solution
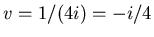 . Thus
. Thus 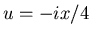 ,
,
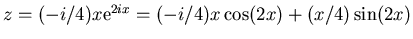 , and
, and
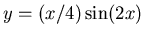 .
Since
.
Since 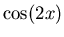 and
and 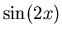 are a fundamental set of solutions
of the homogeneous equation, we get
the general solution
are a fundamental set of solutions
of the homogeneous equation, we get
the general solution
Robert Israel
2002-03-09