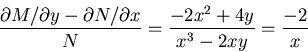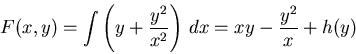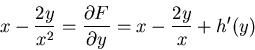The equation is not linear, separable, or exact:
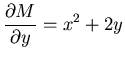 while
while
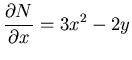 .
But
.
But
is a function of x alone. Therefore we will have an integrating factor that is
a function of x.
We solve
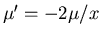 to obtain
to obtain
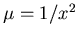 .
Multiplying the equation by
.
Multiplying the equation by 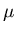 ,
y + y2/x2 + (x - 2 y/x) y' = 0 is exact.
,
y + y2/x2 + (x - 2 y/x) y' = 0 is exact.
so h'(y) = 0 and h(y) = 0. The general solution is
x y - y2/x =C. However, it is impossible to satisfy the initial condition because
this is not defined for x=0. In fact, we might have saved ourselves a lot of work
by being clever enough to notice at the start
that substituting x=0, y=1 into the
differential equation yields 1 = 0.
Robert Israel
2002-02-07
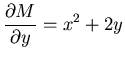 while
while
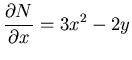 .
But
.
But
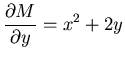 while
while
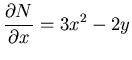 .
But
.
But