9

The differential equation for the population y(t) as a function of time t (measured in years) is y' = a y - b y², where a and b are constants. When y = 10000 we have a y = 20000, so a = 2, and b y² = 10000, so b = 0.0001.

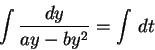
(a) The D.E. can be written as a logistic equation y' = r y (1 - y/K) where r = a = 2 and K = a/b = 20000. Assuming the population starts out at some positive value (not 0), it approaches the stable equilibrium K = 20000.

(b) Solving this separable equation:

$$\int \frac{dy}{a y - b y^2} = \int \, dt$$

$$\frac{\ln y - \ln(a - b y)}{a} = t + C$$

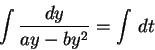
We take t=0 when y = 10000, and $$C = (\ln(10000) - \ln(1))/2 = \ln(10000)/2$$. Then when y = 15000 we have $$t = (\ln(15000) - \ln(1/2))/2 - \ln(10000)/2 = \ln(3)/2 \approx 0.549306$$ years.