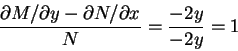
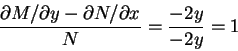
This does not depend on y, so there is an integrating factor ![]() that depends only on x, with
that depends only on x, with
![]() .
A solution of this is
.
A solution of this is
![]() .
.
Now the solution is
F(x,y) = C where
![]() and
and
![]() .
Integrating
.
Integrating ![]() with respect to x, we have
with respect to x, we have
Differentiating with respect to y,
![]() so h'(y) = 0 and we can take h(y) = 0. Thus the general solution is
so h'(y) = 0 and we can take h(y) = 0. Thus the general solution is
![]() .
From the initial value,
.
From the initial value,
![]() .
We can solve for y explicitly:
.
We can solve for y explicitly:
![]() .
Since y(2) = 1 and not -1 we must use +, not -:
.
Since y(2) = 1 and not -1 we must use +, not -: