It must be (b). The given curve has a vertical tangent
somewhere in the first quadrant.
This eliminates (a), for which
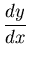 is always finite. The curve has
negative slope at some points in the first quadrant (with y large), and
positive slope at others (with y small). The line separating the two regions
could not be x = y (which eliminates (c)), although it could be x y = 1 as
in (b). Another way to eliminate (c) is to consider the second quadrant
(x < 0, y > 0), where (c) would have
is always finite. The curve has
negative slope at some points in the first quadrant (with y large), and
positive slope at others (with y small). The line separating the two regions
could not be x = y (which eliminates (c)), although it could be x y = 1 as
in (b). Another way to eliminate (c) is to consider the second quadrant
(x < 0, y > 0), where (c) would have
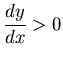 .
Some students
considered a limit as
.
Some students
considered a limit as
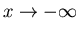 and
and
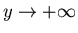 .
In (b), since
.
In (b), since
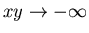 ,
we would have
,
we would have
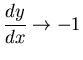 (which fits the picture),
while in (c) with
(which fits the picture),
while in (c) with
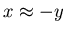 we would get
we would get
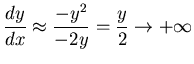 .
.
Robert Israel
2002-02-07
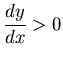 .
Some students
considered a limit as
.
Some students
considered a limit as
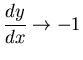 (which fits the picture),
while in (c) with
(which fits the picture),
while in (c) with
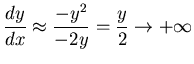 .
.