- 1.
- Show that y is an integrating factor of
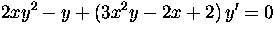 . Find the solutions
F(x,y) = constant.
Solution
. Find the solutions
F(x,y) = constant.
Solution
- 2.
- Find the general solutions of
(a) 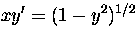 Solution
Solution
(b) 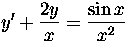 Solution
Solution
(c) 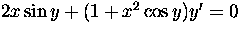 Solution
Solution
(d) 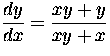 Solution
Solution
- 3.
- Initially a tank contains 1 litre of water and 2 grams of salt. A mixture
containing 1 gram/litre flows in at the rate of 2 litres/min. The stirred mixture
from the tank flows out at 1 litre/min. Find the concentration of salt in the
tank as a function of time. What is the limiting concentration for large time
(and a large tank)?
Solution
- 4.
- Find (if possible) a solution that satisfies the initial condition
y(0) = 1.
(a) 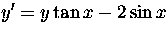 Solution
Solution
(b) 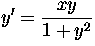 Solution
Solution
(c) 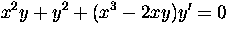 Solution
Solution
- 5.
- An object of mass m is dropped from rest subject to the gravitational
force mg and also an air resistance force proportional to the magnitude of the
velocity.
(a) Find the velocity of the object at any time t.
Solution
(b) Find the time at which the velocity reaches 80% of its limiting
velocity as 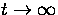 . Leave your answer expressed
in terms of physical constants
and logarithms.
Solution
. Leave your answer expressed
in terms of physical constants
and logarithms.
Solution
- 6.
- Solve the initial value problem
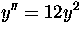 , y(0) = 2, y'(0) = 8.
(Hint: write a differential equation for v = y' as a function of y).
On what interval is the solution defined?
Solution
, y(0) = 2, y'(0) = 8.
(Hint: write a differential equation for v = y' as a function of y).
On what interval is the solution defined?
Solution
- 7.
- The curve shown here constitutes two solutions of one of the following
three differential equations. Why two solutions rather than one?
Which equation is it? State your reasons.
Note: don't try to solve the equations.
Solution
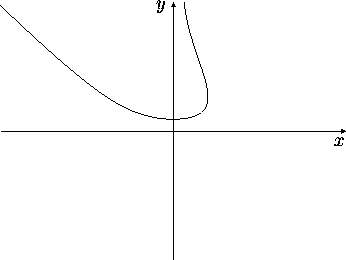
(a) 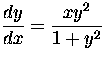
(b) 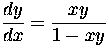
(c) 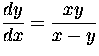
- 8.
- Solve the initial value problems:
(a) 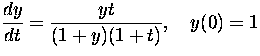 Solution
Solution
(b) 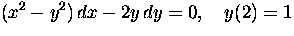
Hint: the equation can be made exact by multiplication by an integrating factor
which depends only on x
Solution
- 9.
- In a certain animal population, the number of births per unit time is
proportional to the population, but the number of deaths per unit time is
proportional to the square of the population. When the population was
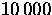 , there were
, there were 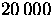 births per year and
births per year and 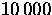 deaths per year.
deaths per year.
(a) What happens to the population in the long run?
(b) How long does it take for the population to go from 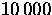 to
to 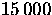 ?
?
Solution
![]() Solution
Solution
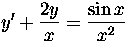 Solution
Solution
![]() Solution
Solution
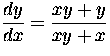 Solution
Solution
![]() Solution
Solution
![]() Solution
Solution
![]() Solution
Solution
![]() . Leave your answer expressed
in terms of physical constants
and logarithms.
Solution
. Leave your answer expressed
in terms of physical constants
and logarithms.
Solution
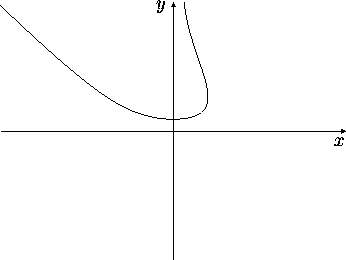
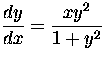
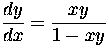
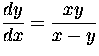
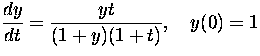 Solution
Solution
![]()
![]() to
to ![]() ?
?