1. [ 6 pts ] The direction field of a differential equation
1. [ 6 pts ] The direction field of a differential equation ![]() is shown
below. Sketch the isocline
is shown
below. Sketch the isocline ![]() and the solution curve with
and the solution curve with ![]() .
Will they meet?
.
Will they meet?
The isocline is shown in red and the solution curve in blue.
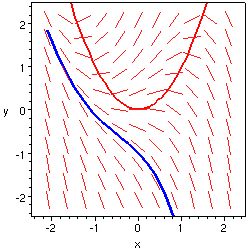
They will not meet (unless the isocline unexpectedly takes a downward turn somewhere to the left of the part that is shown).
2. [ 12 pts ] For what value of the constant ![]() is the differential equation
is the differential equation
The test for exactness is
![]() .
With
.
With ![]() and
and ![]() , that is
, that is ![]() .
.
With ![]() , the solution is
, the solution is ![]() where
where
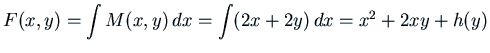 .
Then
.
Then
![]() , so
, so ![]() . Note that this depends only on
. Note that this depends only on ![]() - if it didn't, we'd know that we'd
made a mistake somewhere. Then
- if it didn't, we'd know that we'd
made a mistake somewhere. Then
![]() . From the initial condition,
. From the initial condition,
![]() , so the solution (in implicit form) is
, so the solution (in implicit form) is
![]() .
.
3. [ 12 pts ] A tank initially contains 200 litres of fresh water. Then a salt solution of unknown concentration is poured into the tank at a steady rate of 2 litres per minute, and the well-stirred mixture is drained out at the same rate. After 120 minutes the concentration of salt in the tank is 15 grams per litre. What is the concentration of the salt solution entering the tank?
The volume of liquid in the tank is constant. Salt enters the tank at
a rate of ![]() grams per minute, where
grams per minute, where ![]() is the concentration of the
solution entering the tank.
The differential equation for the amount
is the concentration of the
solution entering the tank.
The differential equation for the amount ![]() of salt in the tank is
of salt in the tank is
4. [ 10 pts ] Using the Improved Euler method to approximate
the solution at ![]() of an initial value problem
of an initial value problem ![]() ,
, ![]() ,
I obtained an answer of
,
I obtained an answer of ![]() with step size
with step size
![]() and
and ![]() with step size
with step size ![]() . What step size should I
try if I want the error to be approximately
. What step size should I
try if I want the error to be approximately ![]() ?
?
The global error for Improved Euler is approximately proportional to ![]() .
The Richardson Extrapolation value for
.
The Richardson Extrapolation value for ![]() is
is
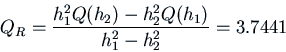
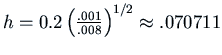 .
.