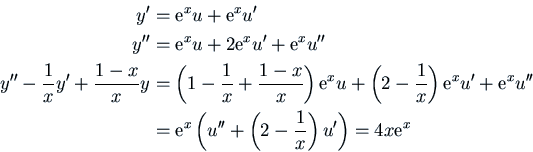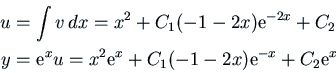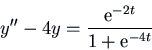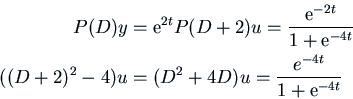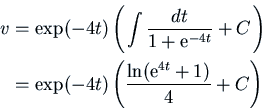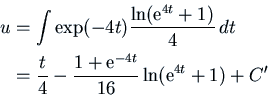Non-Constant Coefficients: Reduction of Order
Second-order linear equations with non-constant coefficients don't always
have solutions that can be expressed in ``closed form'' using the functions
we are familiar with. However, if you know one nonzero
solution of the homogeneous equation you can find the general solution
(both of the homogeneous and non-homogeneous equations).
The basic idea is to write a solution as 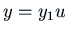 where
where
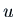 is some function of
is some function of 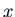 . What equation must
. What equation must 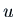 satisfy?
satisfy?
To find out, we plug in 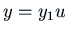 to the left side of the differential
equation.
to the left side of the differential
equation.
We will still have a second order linear differential equation for 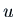 ,
but since this only depends on
,
but since this only depends on 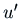 and
and 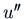 we can think of it as
a first-order linear differential equation for
we can think of it as
a first-order linear differential equation for 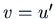 . We know how
to solve first-order linear differential equations
(assuming we can do the required integrations), so we will
be able to find
. We know how
to solve first-order linear differential equations
(assuming we can do the required integrations), so we will
be able to find 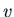 . Then we integrate to get
. Then we integrate to get 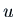 , and we have
our solution
, and we have
our solution 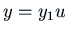 .
.
Example: Solve the non-homogeneous equation
for  ,
given that
,
given that
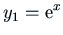 is one solution of the homogeneous equation
is one solution of the homogeneous equation
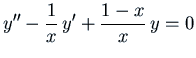 .
.
Taking
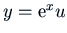 , we have
, we have
Thus the equation for 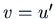 is
is
The integrating factor is
so the general solution is
Integrating, we get
Note that we get the general solution: the second fundamental solution
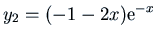 of the homogeneous equation
comes from the constant
of the homogeneous equation
comes from the constant 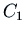 in the integration that gives us
in the integration that gives us 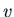 . The constant
. The constant 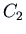 in the last integration leads to the first fundamental solution (which we
already knew).
in the last integration leads to the first fundamental solution (which we
already knew).
Here's an example with a constant-coefficient equation. The idea is the
same, but the Exponential Shift technique makes it easier.
Of course, there is still no guarantee that we will be able to find the
integrals in closed form.
Example: Find a solution of the differential equation
The roots of the characteristic polynomial are 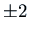 . So let's
look
for a particular solution of the form
. So let's
look
for a particular solution of the form
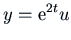 .
Exponential Shift gives us
.
Exponential Shift gives us
Writing 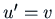 , we have
, we have
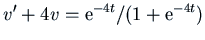 .
The integrating
factor is
.
The integrating
factor is
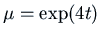 . The solution to this first-order
linear equation is
. The solution to this first-order
linear equation is
We just need a particular solution, so take  .
Integrating (it's not an easy integral):
.
Integrating (it's not an easy integral):
Again, we can ignore the constant  , and our particular solution is
, and our particular solution is
Robert Israel
2002-03-09
![]() where
where
![]() is some function of
is some function of ![]() . What equation must
. What equation must ![]() satisfy?
satisfy?
![]() to the left side of the differential
equation.
to the left side of the differential
equation.
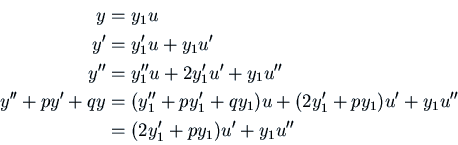
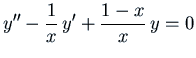 .
.
![]() , we have
, we have