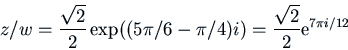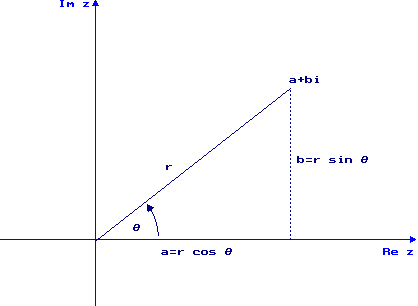
Consider the complex number ![]() , corresponding to point
, corresponding to point ![]() in the
plane. Its polar coordinates are
in the
plane. Its polar coordinates are ![]() and
and ![]() , where
, where ![]() is the distance
from the origin and
is the distance
from the origin and ![]() is the counterclockwise angle from the positive
real axis to the point. We have
is the counterclockwise angle from the positive
real axis to the point. We have
![]() and
and
![]() , so
, so
For example, if we want to represent
![]() in polar coordinates, we first
calculate
in polar coordinates, we first
calculate
![]() so
so ![]() . Then we want
. Then we want
![]() and
and
![]() . The angle with
this sine and this cosine in the interval
. The angle with
this sine and this cosine in the interval ![]() to
to ![]() is
is ![]() . So the polar
representation is
. So the polar
representation is
![]() .
.
The polar representation is especially useful for multiplication and division of
complex numbers. If
![]() and
and
![]() then
then
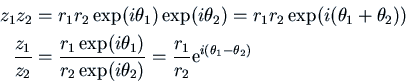
For example, let's divide ![]() by
by
![]() .
We have
.
We have
![]() since
since
![]() .
So
.
So