Here are some of the principles of trajectory sketching:
The linear approximation to a function of two variables ![]() near a
point
near a
point ![]() is
is
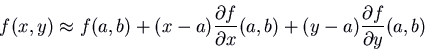
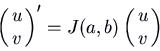
Example: Consider the system
![]() ,
,
![]() .
.
For an equilibrium point we need ![]() (i.e.
(i.e. ![]() or
or ![]() ) and
) and
![]() (i.e.
(i.e. ![]() or
or ![]() ). There are thus two equilibrium points:
). There are thus two equilibrium points:
![]() and
and ![]() .
.
Before classifying the equilibrium points, it's a good idea to draw the
isoclines for ![]() and
and ![]() . I'll plot the first in blue and the
second in green.
I indicate with arrows the direction field in each region and on the
isoclines. The intersections of the blue and green isoclines are the
equilibrium points.
. I'll plot the first in blue and the
second in green.
I indicate with arrows the direction field in each region and on the
isoclines. The intersections of the blue and green isoclines are the
equilibrium points.

The Jacobian matrix is
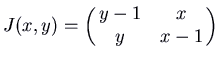 . At the equilibrium point
. At the equilibrium point
![]() this is
this is
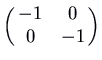 . That has
a double eigenvalue
. That has
a double eigenvalue ![]() , and two linearly independent eigenvectors.
Therefore the equilibrium point
, and two linearly independent eigenvectors.
Therefore the equilibrium point ![]() is a singular node, and is an
attractor.
is a singular node, and is an
attractor.
At the second equilibrium point ![]() the Jacobian matrix is
the Jacobian matrix is
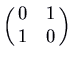 . This has eigenvalues 1 and
. This has eigenvalues 1 and ![]() .
Therefore the equilibrium point
.
Therefore the equilibrium point ![]() is a saddle. The eigenvectors
are
is a saddle. The eigenvectors
are
![]() for 1 and
for 1 and
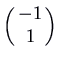 for
for ![]() . The picture below shows the phase plane with
some parts of trajectories near the two equilibrium points. Note that
the directions of these trajectories agree with the direction field
arrows from the previous picture.
. The picture below shows the phase plane with
some parts of trajectories near the two equilibrium points. Note that
the directions of these trajectories agree with the direction field
arrows from the previous picture.

Now we sketch some trajectories.
There are trajectories on the ![]() and
and ![]() axes (going inwards to the equilibrium
point at the origin), because
axes (going inwards to the equilibrium
point at the origin), because ![]() when
when ![]() and
and ![]() when
when ![]() .
Next it's a good idea to sketch the
trajectories coming out of and going in to the saddle point.
For example, one comes in to the saddle point from below and to the right.
We go backwards in time, following the arrows backward. These arrows
point up and left in the region
.
Next it's a good idea to sketch the
trajectories coming out of and going in to the saddle point.
For example, one comes in to the saddle point from below and to the right.
We go backwards in time, following the arrows backward. These arrows
point up and left in the region ![]() ,
, ![]() . The trajectory
must curve to avoid the trajectory on the positive
. The trajectory
must curve to avoid the trajectory on the positive ![]() axis. It is
presumably asymptotic to that axis. The trajectory coming out of the
saddle point down and to the left must continue down and to the left
until it ends at the equilibrium point
axis. It is
presumably asymptotic to that axis. The trajectory coming out of the
saddle point down and to the left must continue down and to the left
until it ends at the equilibrium point ![]() .
.

Finally, we draw some more trajectories, including at least one in each region.
Note that those trajectories that enter the equilibrium point at ![]() can do so at any angle.
can do so at any angle.

Our picture is symmetric about the line ![]() , because of the fact that the
system of equations remains the same if you interchange
, because of the fact that the
system of equations remains the same if you interchange ![]() and
and ![]() .
.
The trajectories entering and leaving the saddle point are separatrices.
All trajectories below and to the left of the two trajectories entering
the saddle go to the equilibrium point ![]() as
as ![]() , while those
above and to the right go off to infinity asymptotic to the line
, while those
above and to the right go off to infinity asymptotic to the line ![]() .
Below and to the right of the trajectories leaving the saddle, everything
comes in from
infinity asymptotic to the positive
.
Below and to the right of the trajectories leaving the saddle, everything
comes in from
infinity asymptotic to the positive ![]() axis (as
axis (as ![]() ),
while above and to the left
of these everything comes in from infinity asymptotic to the positive
),
while above and to the left
of these everything comes in from infinity asymptotic to the positive ![]() axis.
axis.
As I mentioned, there are two exceptions to the rule that the phase portrait
near an equilibrium point can be classified by the
linearization at that equilibrium point. The first is where 0 is an
eigenvalue of the linearization (we didn't even look at the linear system
in that case!).
The second exception is where
the linearization is a centre. The linear system has periodic solutions,
corresponding to trajectories that are closed curves (ellipses). Imagine
starting at some point and following the direction field. After going
all the way around the equilibrium point, in the linear system you return
exactly to the point you started at. This is a very delicate matter,
and any nonlinear effect, even if very small, could spoil it. If in
the nonlinear system you come
back slightly farther away from the equilibrium point than where you started,
then your trajectory can not be a closed curve. The next time around, you
will be still farther away. The trajectory will spiral away from the
equilibrium point. If all trajectories
near the equilibrium point are like this, the equilibrium point is an unstable spiral.
On the other hand, if after one turn around the equilibrium point you are
slightly closer than where you started, your trajectory spirals inwards.
If all trajectories near the equilibrium point are like this, the equilibrium point
is a stable spiral (and an attractor).
Here are pictures of those two possibilities. The third possibility, of course,
is that you do come back exactly to the point where you started,
and it really is a centre.


One way to show that a centre of the linearized system is
still a centre in the nonlinear system is to find an equation for
the trajectories. If there is such an (implicit) equation ![]() where
where ![]() is a smooth function, not constant in any region,
and
is a smooth function, not constant in any region,
and ![]() an arbitrary constant, then the trajectories, which are level curves of
this function, can not be spirals but can be closed curves. This occurs
both in the predator-prey and pendulum systems.
an arbitrary constant, then the trajectories, which are level curves of
this function, can not be spirals but can be closed curves. This occurs
both in the predator-prey and pendulum systems.