Logistic Growth

Consider a model for changes in population of some creature (perhaps bacteria, animals or people) as a function of time. Let y(t) be the number of creatures at time t. Of course y(t) can only take integer values, but for the sake of our model we can ignore that (it shouldn't matter too much if the populations are large). There are two processes that affect the population: birth and death.

$$y' = \mbox{(births per unit time)} - \mbox{ (deaths per unit time)}$$

In the simplest model, both the number of births per unit time and the number of deaths per unit time are simply proportional to the population: $\beta y$ and $\gamma y$, where $\beta$and $\gamma$ are called the birth rate and the death rate. This would occur if in a small interval of time $\Delta t$ each individual has approximately constant probabilities $\beta \Delta t$ of giving birth to a new individual and $\gamma \Delta t$ of dying (the fact that not all individuals can give birth is not a serious difficulty, as long as the proportion of individuals that can is constant). Then the differential equation is

$$y' = \beta y - \gamma y = r y$$

where $r = \beta - \gamma$. This is just the equation of exponential growth (if r > 0) or decay (if r < 0). If r < 0 the population is doomed to die out, so let's suppose that r > 0. However, in any realistic situation exponential growth can not continue indefinitely. Something (typically the limited supply of some resource such as living space or food) must eventually increase the death rate, decrease the birth rate, or both, preventing the population from getting too large. The result should be a new DE of the form

y' = f(y) y

where f(y) is some function of y. We should expect that f(y)is approximately r when y is small, decreases when y grows larger, and is negative when y is sufficiently large. The simplest function of this form is f(y) = r - a y where ais a positive constant. It is convenient to write a = r/K. Then the DE becomes

y' = r (1 - y/K) y

This is called the logistic equation.

Before solving the logistic equation, we'll look at some of its qualitative aspects using the direction field. We can interpret K as follows: when y = K, y' = 0. Thus the constant y=Kis a solution to our DE. A constant solution such as this is called an equilibrium point of the equation. There is one other, perhaps less desirable, equilibrium point: y = 0.

Here are the direction field and some solution curves (this is for r = K = 1, but the picture will be similar for other values of r and K):

Note the two constant solutions y = 0 and y = K. In the region between y = 0 and y = K, the slopes are positive. Any initial condition in this region corresponds to a solution with $y \to K$ as $t \to \infty$, and $y \to 0$ as $t \to -\infty$. In the region y > K the slopes are negative. An initial condition in this region corresponds to a solution with $y \to K$ as $t \to \infty$, and $y \to \infty$ in the backward direction (it turns out, at some finite value of t). The region y < 0 is not very relevant for the application because you can't have a negative population, but note that there we have $y \to -\infty$ in the forward direction (again, as it turns out, at a finite value of t) and $y \to 0$ as $t \to -\infty$. Of the two equilibrium points, y=0 is said to be unstable and y=K is stable.

The logistic equation is separable, so we can solve it.

$$\int \frac{dy}{y (1 - y/K)} = \int r\, dt = rt + C$$

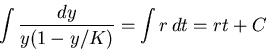
The integral can be done using partial fractions, obtaining

$$\ln \vert y\vert - \ln \vert K - y\vert = r t + C$$

Apply the exponential function to both sides:

$$\left\vert \frac{y}{K-y} \right\vert = {\rm e}^C {\rm e}^{r t}$$

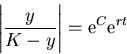
Thus

$$\frac{y}{K-y} = \pm {\rm e}^C {\rm e}^{r t} = A {\rm e}^{r t}$$

where A is an arbitrary constant. Solving for y we get the general solution

$$y = \frac{A K {\rm e}^{r t}}{1 + A {\rm e}^{r t}}$$

Notice, however, that this general solution doesn't actually include the particular solution y = K (that would be the limit of the general solution as $A \to \infty$). Positive values of A correspond to solutions in the region 0 < y < K. A = 0 means y = 0. For a negative value of A, the denominator will be 0 at t = t₀ where $\exp(r t_0) = -1/A$. Such an A actually corresponds to two solution curves. For t < t₀, we have a solution with y < 0 and $y \to -\infty$ as $t \to t_0-$. For t > t₀, we have a solution with y > K and $y \to +\infty$ as $t \to t_0+$. This justifies the previous remarks about ``some finite value of t.''