Integration by Undetermined Coefficients

In the last page we had to integrate $$\int t {\rm e}^{3 t}\, dt$$.

The usual Math 101 method for doing this is integration by parts. However, there is another method that's more in the spirit of this course, which you may find more convenient for integrals of this type: the Method of Undetermined Coefficients.

The idea behind the method is very simple: start by writing down a general form of the antiderivative, take the derivative of a function of this form, and see what the coefficients have to be to make it work. In this case the general form of the antiderivative is the following:

If p(t) is a polynomial of degree n (i.e. the highest power of t that occurs in it is tⁿ) and c is a nonzero constant, then $$\int p(t) {\rm e}^{ct} \, dt = q(t) {\rm e}^{ct} + C$$ where q(t) is also a polynomial of degree n.

For $$\int t {\rm e}^{3 t}\, dt$$, p(t)=t is a polynomial of degree 1, and so q(t) = A₁ t + A₀, where A₁ and A₀ are the coefficients to be determined. Taking the derivative:

$$\frac{d}{dt} \left( (A_1 t + A_0) {\rm e}^{3 t} \right) = ... ... A_0) {\rm e}^{3t} = (3 A_1 t + (A_1 + 3 A_0)) {\rm e}^{3t} + C$$

Now this is supposed to be the same as $$t {\rm e}^{3t}$$. The only way that can happen is for the coefficients of each power of t to match: 3 A₁ must be the same as 1, and A₁ + 3 A₀ must be 0. From 3 A₁ = 1 we get A₁ = 1/3, and then from A₁ + 3 A₀ = 0 we get A₀ = -1/9. So the conclusion is

$$\int t {\rm e}^{3t}\, dt = \left ( \frac{t}{3} - \frac{1}{9}\right) {\rm e}^{3t} + C$$

Let's try a more complicated one: $$\int (t^3 - 2 t) {\rm e}^{-2 t}\, dt$$. The antiderivative is of the form $$(A_3 t^3 + A_2 t^2 + A_1 t + A_0) {\rm e}^{-2t} + C$$. Differentiating it, we get

$$\displaylines{ (3 A_3 t^2 + 2 A_2 t + A_1) {\rm e}^{-2t} - ... ...A_2) t^2 + (2 A_2 - 2 A_1) t + (A_1 - 2 A_0)) {\rm e}^{-2t}\cr}$$

so equating the coefficients of each power of t:

$$\begin{array} {lll} - 2 A_3 = 1 &\qquad& 3 A_3 - 2 A_2 = 0 \ 2 A_2 - 2 A_1 = -2 & \qquad & A_1 - 2 A_0 = 0 \end{array}$$

Thus (always starting with the coefficient of the highest power of t) A₃ = -1/2, A₂ = - 3/4, A₁ = 1/4, A₀ = 1/8, and the answer is

$$\left( -\frac{1}{2} t^3 - \frac{3}{4} t^2 + \frac{1}{4} t + \frac{1}{8} \right) {\rm e}^{-2t} + C$$

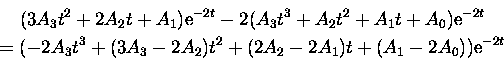
Try this by integration by parts, if you want to see how much more efficient Undetermined Coefficients is for this problem!