Integrating Factors

Suppose we have a differential equation M(x,y) + N(x,y) y' = 0 that is not exact. It may be that we can convert it into an exact equation by multiplying it by some function $\mu(x,y)$. Such a function is called an integrating factor. In fact, this is just what we did for the linear equation.

What is needed for $\mu(x,y)$ to be an integrating factor? Apply the test for exact equations to $\mu M + \mu N y' = 0$:

$$\frac{\partial(\mu M)}{\partial y} = \frac{\partial(\mu N)}{\partial x}$$

Unfortunately, in general it's just as hard to solve this for $\mu$ as it is to solve the original differential equation. But in some special cases it is easier. For example, suppose $\mu$ depends only on x. The exactness test becomes

$$\mu \frac{\partial M}{\partial y} = \mu \frac{\partial N}{\partial x} + \mu' N$$

$$\mu'/\mu = \frac{\partial M/\partial y - \partial N/\partial x}{N}$$

The left side is supposed to depend only on x, so the right side must also depend only on x. That is the requirement for the equation to have an integrating factor that depends only on x. If this requirement is fulfilled, we have a first-order homogeneous linear equation to solve for $\mu$.

Example: Solve x²+ y³ + (x² - 3 x y²) y' = 0.

We have M = x²+ y³, N = x² - 3 x y². Since

$$\frac{\partial M}{\partial y} = 3 y^2 {\rm\ \ while \ \ } \frac{\partial N}{\partial x} = 2 x - 3 y^2$$

the equation is not exact. However,

$$\frac{\partial M/\partial y - \partial N/\partial x}{N} = \frac{- 2 x + 6 y^2 }{ x^2 - 3 x y^2} = - \frac{2}{x}$$

depends only on x, so there is an integrating factor that depends on x. The equation for that integrating factor is

$$\mu' = - 2 \mu/x$$

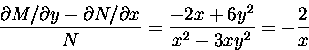
Solving this, we get

$$\mu(x) = \exp\left(-\int \frac{2}{x}\, dx\right) = \exp(- 2 \ln x) = \frac{1}{x^2}$$

So our exact equation is

$$\frac{x^2 + y^3}{x^2} + \left(1 - \frac{3 y^2}{x}\right) y' = 0$$

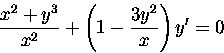
Now if the solution is F(x,y) = C, we want

$$\displaystyle \frac{\partial F}{\partial x} = 1 +\frac{ y^3}{x^2}$$

$$\displaystyle F = x - \frac{y^3}{x} + K(y)$$

$$\displaystyle \frac{\partial F}{\partial y} = - \frac{3 y^2}{x} + K'(y) = 1 - \frac{3 y^2}{x}$$

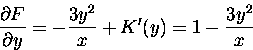
K'(y) = 1

K(y) = y

Thus the solution is

$$x - \frac{y^3}{x} + y = C$$