Many differential equations have solutions that can be written in implicit form:
F(x,y) = C
Now instead of starting with the differential equation and finding the solution, suppose we look at this ``backwards'': start with the solution F(x,y) = C and differentiate it, obtaining a differential equation. For example, the solutions
y2 + x y = C
would lead to the differential equation![]()
In general, we have (with y = y(x))
![]()
An equation of the form
![]()
Now let's look ``forwards'' again: we have a differential equation which we suspect might be exact. We need to be able to
Thus we want to be able to look at the differential equation
![]() and see that
and see that ![]() and
and ![]() where F = x y + y2,
and therefore that the general solution is x y + y2 = C.
where F = x y + y2,
and therefore that the general solution is x y + y2 = C.
The test for exactness comes from the equality of mixed partial derivatives:
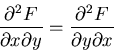
![]()
![]()
Suppose M, N,and
are continuous in a rectangular region R: a < x < b, c < y < d. Then the differential equation
is exact in R (i.e. there is a function F defined in R with
and
there) if and only if
everywhere in R.
Now how do we find F when the equation is exact? By
integration. In our example, we want ![]() and
and ![]() . Look at the first
equation, and integrate with respect to x:
. Look at the first
equation, and integrate with respect to x:
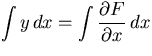
A few points to notice:
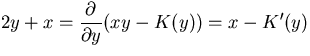
This time the ``constant'' c really is constant, and we can ignore it (since at the end the solution F(x,y) = C will have a constant in it anyway). We conclude that F(x,y) = x y + y2 = C is the general solution of our differential equation.
Thus you can use the following procedure for solving an exact equation:
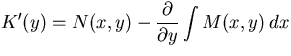 . Make sure this is a function
of y only, with no x in it (after whatever simplifications are necessary). If
it does depend on x, you've made a mistake somewhere.
. Make sure this is a function
of y only, with no x in it (after whatever simplifications are necessary). If
it does depend on x, you've made a mistake somewhere.