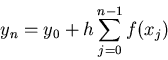Error Analysis of the Euler Method
As before, we are considering the first-order initial value problem
and approximating its solution using Euler's method with a certain
step size 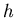 . I will ignore roundoff error and consider only the
discretization error.
For
step-by-step methods such as Euler's for solving ODE's, we want to
distinguish between two types of discretization
error: the global error and the local error.
The global error at a certain value of
. I will ignore roundoff error and consider only the
discretization error.
For
step-by-step methods such as Euler's for solving ODE's, we want to
distinguish between two types of discretization
error: the global error and the local error.
The global error at a certain value of 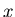 (assumed to be
(assumed to be
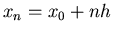 )
is just what we would ordinarily call the error: the difference between
the true value
)
is just what we would ordinarily call the error: the difference between
the true value 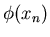 and the approximation
and the approximation 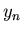 .
The local error at
.
The local error at 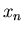 is, roughly speaking, the error introduced in
the
is, roughly speaking, the error introduced in
the 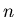 th step of the process. That is, it is the difference between
th step of the process. That is, it is the difference between
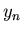 and
and
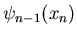 , where
, where 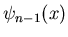 is the solution
of the differential equation with
is the solution
of the differential equation with
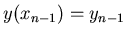 . Thus if
. Thus if
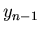 were exactly correct (equal to
were exactly correct (equal to 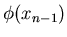 ), the global
error at
), the global
error at 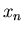 would be equal to this local error. But since in
general
would be equal to this local error. But since in
general 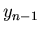 is not correct (as a result of earlier local errors),
the global and local errors are different.
In the picture below,
is not correct (as a result of earlier local errors),
the global and local errors are different.
In the picture below, 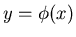 is the black curve,
and the curves
is the black curve,
and the curves 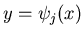 are in red.
The local errors at each stage of the process
are the blue vertical lines.
are in red.
The local errors at each stage of the process
are the blue vertical lines.
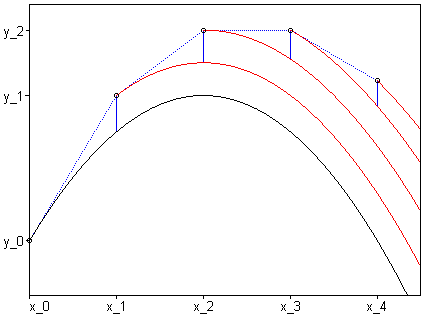
First we consider the local error at 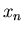 :
:
Now
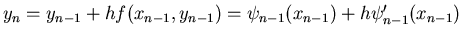 . According to Taylor's Theorem, for any
twice-differentiable function
. According to Taylor's Theorem, for any
twice-differentiable function 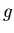
for some 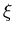 between
between 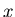 and
and 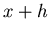 . Taking
. Taking
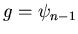 ,
, 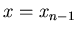 and
and 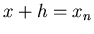 we find
we find
If there is some constant 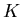 such that we can be sure that
such that we can be sure that
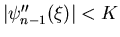 , then we can say
, then we can say
Such a 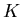 does exist (assuming
does exist (assuming 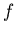 has continuous derivatives in some
rectangle containing the true and approximate solutions):
for any solution of the differential equation
has continuous derivatives in some
rectangle containing the true and approximate solutions):
for any solution of the differential equation 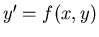 , we can differentiate
once more to get
, we can differentiate
once more to get
which is a continuous function of 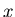 and
and 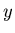 and therefore
can't get too big in our rectangle.
and therefore
can't get too big in our rectangle.
Now, what about the global error? It's tempting to say that the
global error at 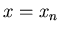 is the sum of all the local errors
is the sum of all the local errors 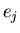 for
for
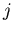 from 1 to
from 1 to 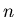 . Since each
. Since each 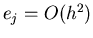 and there are
and there are
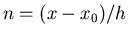 of them, the global error should be
of them, the global error should be
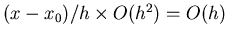 .
Unfortunately, it's not quite true that the global error is the sum of the
local errors: the global error at
.
Unfortunately, it's not quite true that the global error is the sum of the
local errors: the global error at 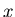 is the sum of the differences
is the sum of the differences
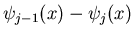 , but
, but
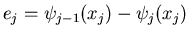 .
Between
.
Between 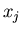 and
and 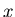 ,
,
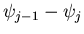 might grow or shrink.
Fortunately, we can control the amount of growing that might take
place, and the result is that it grows by at most some constant factor
(again, this is in a rectangle where
might grow or shrink.
Fortunately, we can control the amount of growing that might take
place, and the result is that it grows by at most some constant factor
(again, this is in a rectangle where 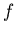 has continuous derivatives and
which contains the true and approximate solutions).
has continuous derivatives and
which contains the true and approximate solutions).
Let's look at a simple example: 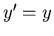 ,
, 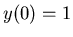 . This is so simple
that we can find an explicit formula for
. This is so simple
that we can find an explicit formula for 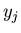 . We have
. We have
Thus at each stage 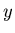 is multiplied by
is multiplied by 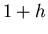 . Since we start out with
. Since we start out with
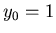 , we have
, we have
The actual solution is of course
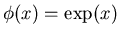 . The
global error at
. The
global error at 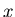 with step size
with step size 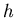 , where
, where 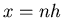 , is
, is
Since
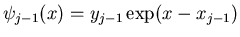 the local error in step
the local error in step 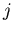 is
is
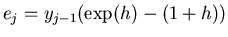 .
.
The local error is 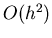 because (from Taylor series)
because (from Taylor series)
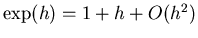 . The global error is
. The global error is 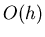 : in fact,
on the
O and Order page, we used the example
: in fact,
on the
O and Order page, we used the example
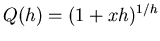 , which we saw had error
, which we saw had error 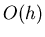 . The
Euler approximation is just
. The
Euler approximation is just 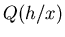 , so it too has error
, so it too has error 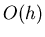 .
.
Another special case: suppose 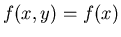 is just a function of
is just a function of 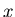 .
The true solution is
.
The true solution is
For the Euler method we have
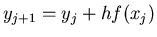 , so that
, so that
This is a just a Riemann sum for the integral: for each interval
![$[x_j, x_{j+1}]$](img64.png) we are approximating the area under the graph of
we are approximating the area under the graph of
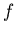 by a rectangle with height
by a rectangle with height 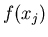 . As you may have seen in
calculus, the error in this approximation for each interval is
at most
. As you may have seen in
calculus, the error in this approximation for each interval is
at most 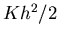 if
if 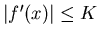 on the interval, and the global
error at
on the interval, and the global
error at 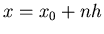 is then at most
is then at most
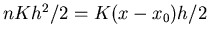 .
.
Robert
2002-01-28

![]() :
:
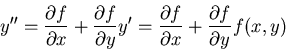
![]() is the sum of all the local errors
is the sum of all the local errors ![]() for
for
![]() from 1 to
from 1 to ![]() . Since each
. Since each ![]() and there are
and there are
![]() of them, the global error should be
of them, the global error should be
![]() .
Unfortunately, it's not quite true that the global error is the sum of the
local errors: the global error at
.
Unfortunately, it's not quite true that the global error is the sum of the
local errors: the global error at ![]() is the sum of the differences
is the sum of the differences
![]() , but
, but
![]() .
Between
.
Between ![]() and
and ![]() ,
,
![]() might grow or shrink.
Fortunately, we can control the amount of growing that might take
place, and the result is that it grows by at most some constant factor
(again, this is in a rectangle where
might grow or shrink.
Fortunately, we can control the amount of growing that might take
place, and the result is that it grows by at most some constant factor
(again, this is in a rectangle where ![]() has continuous derivatives and
which contains the true and approximate solutions).
has continuous derivatives and
which contains the true and approximate solutions).
![]() ,
, ![]() . This is so simple
that we can find an explicit formula for
. This is so simple
that we can find an explicit formula for ![]() . We have
. We have
![]() because (from Taylor series)
because (from Taylor series)
![]() . The global error is
. The global error is ![]() : in fact,
on the
O and Order page, we used the example
: in fact,
on the
O and Order page, we used the example
![]() , which we saw had error
, which we saw had error ![]() . The
Euler approximation is just
. The
Euler approximation is just ![]() , so it too has error
, so it too has error ![]() .
.
![]() is just a function of
is just a function of ![]() .
The true solution is
.
The true solution is