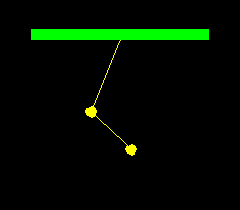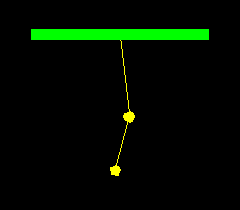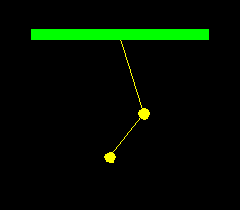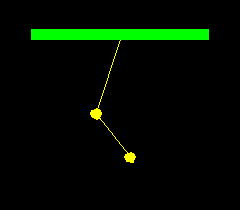
A double pendulum consists of two balls hanging from strings:
a string of length ![]() connects a fixed support to a ball
of mass
connects a fixed support to a ball
of mass ![]() , and a string of length
, and a string of length ![]() connects this ball
to another ball of mass
connects this ball
to another ball of mass ![]() . We will assume that the objects
are hanging almost vertically and swinging slowly, so that we can
use a linear approximation to their motion.
. We will assume that the objects
are hanging almost vertically and swinging slowly, so that we can
use a linear approximation to their motion.
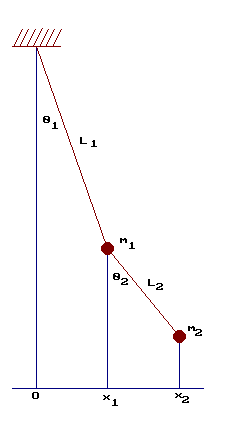
Let ![]() and
and ![]() be the angles of the two strings from
the vertical. If
be the angles of the two strings from
the vertical. If ![]() and
and ![]() are the
are the ![]() coordinates of the
two objects, where
coordinates of the
two objects, where ![]() is directly below the support,
we have
is directly below the support,
we have
![]() and
and
![]() .
Since the angles are small, we can approximate
.
Since the angles are small, we can approximate
![]() and
and
![]() . The tensions in the
strings are
. The tensions in the
strings are
![]() and
and
![]() respectively (the second string supports the weight of one ball, while
the first string supports two; the weight of the strings is neglected).
The net force in the
respectively (the second string supports the weight of one ball, while
the first string supports two; the weight of the strings is neglected).
The net force in the ![]() direction on the first ball is then
direction on the first ball is then
![]() ,
while the net force in the
,
while the net force in the ![]() direction on the second ball is
direction on the second ball is
![]() . According to Newton's Laws,
these forces are equal to
. According to Newton's Laws,
these forces are equal to ![]() and
and ![]() respectively.
Writing these in terms of
respectively.
Writing these in terms of ![]() and
and ![]() , and using the
approximations again, we have
, and using the
approximations again, we have
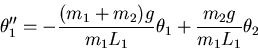
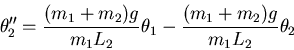
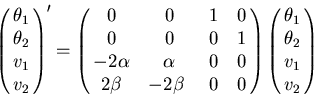
Thus we need four linearly independent solutions to make a fundamental set.
But it's easier to work with our 2 by 2 matrix ![]() instead of a 4 by 4 matrix.
If we take
instead of a 4 by 4 matrix.
If we take
![]() where
where ![]() is a constant vector, then
is a constant vector, then
![]() , so this is
a solution if
, so this is
a solution if
![]() , i.e.
, i.e. ![]() is an eigenvector of
is an eigenvector of ![]() for eigenvalue
for eigenvalue
![]() . Assuming our matrix
. Assuming our matrix ![]() has two distinct eigenvalues, neither of them
0, each eigenvalue has two square roots, and this will give us our four
linearly independent solutions.
has two distinct eigenvalues, neither of them
0, each eigenvalue has two square roots, and this will give us our four
linearly independent solutions.
For ease of calculation, let's try ![]() and
and ![]() . The characteristic
equation of
. The characteristic
equation of
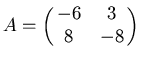 is
is
![]() .
The eigenvalues are thus
.
The eigenvalues are thus ![]() and
and ![]() . The corresponding eigenvectors
are
. The corresponding eigenvectors
are
![]() and
and
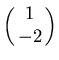 . So our fundamental
set of solutions is
. So our fundamental
set of solutions is
In the physical model I made, the string lengths were ![]() cm and
cm and
![]() cm, so
cm, so
![]() and
and ![]() . The resulting
solutions are
. The resulting
solutions are