Complex Numbers
As we have seen, a second order constant coefficient linear homogeneous
equation
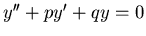 has solutions
has solutions 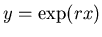 , where
, where
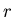 is a root of the quadratic equation
is a root of the quadratic equation
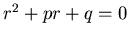 .
Some quadratic equations, such as
.
Some quadratic equations, such as 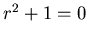 , don't have any real roots.
However, they all have complex roots. In order to study these equations,
we will have to consider
complex numbers.
, don't have any real roots.
However, they all have complex roots. In order to study these equations,
we will have to consider
complex numbers.
A complex number is an expression of the form 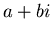 , where
, where 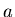 and
and 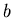 are real numbers and
are real numbers and 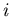 is a special symbol
(Engineers usually use the letter
is a special symbol
(Engineers usually use the letter 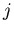 instead of
instead of 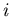 ).
While real numbers can be represented as points on a line, complex numbers
can be represented as points on a plane:
).
While real numbers can be represented as points on a line, complex numbers
can be represented as points on a plane: 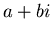 corresponds to the
point
corresponds to the
point 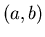 . A real number
. A real number 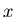 can be consider as the complex number
can be consider as the complex number
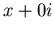 (which we would write as
(which we would write as 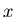 ). Thus in the complex plane, the
``
). Thus in the complex plane, the
``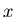 axis'' consists of real numbers: we call it the real axis. The
``
axis'' consists of real numbers: we call it the real axis. The
``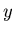 axis'', consisting of the numbers
axis'', consisting of the numbers 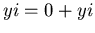 , is called the
imaginary axis, and the numbers on it are imaginary numbers.
The real part of
, is called the
imaginary axis, and the numbers on it are imaginary numbers.
The real part of 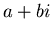 is
is 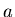 , and the imaginary part is
, and the imaginary part is 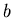 .
Note: in this page
.
Note: in this page 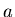 and
and 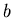 are always assumed to be real numbers.
We write
are always assumed to be real numbers.
We write
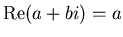 and
and
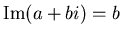 .
Arithmetic of complex numbers follows the usual rules, with the special
property
.
Arithmetic of complex numbers follows the usual rules, with the special
property 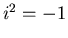 . Thus for addition and subtraction,
. Thus for addition and subtraction,
For multiplication,
e.g.
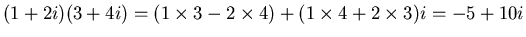 .
Division is a bit more complicated, and requires introducing another
operation:
the complex conjugate of a complex number
.
Division is a bit more complicated, and requires introducing another
operation:
the complex conjugate of a complex number 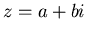 is
is
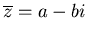 . Note that
. Note that
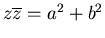 is real. So to divide
is real. So to divide
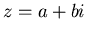 by
by 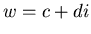 , we multiply numerator and denominator
by
, we multiply numerator and denominator
by 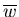 :
:
e.g.
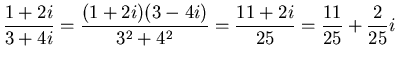 .
Complex conjugation has some important properties. To take the complex
conjugate of any algebraic expression, interchange all complex variables with
their complex conjugates, change every
.
Complex conjugation has some important properties. To take the complex
conjugate of any algebraic expression, interchange all complex variables with
their complex conjugates, change every 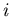 to
to 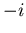 , and leave real numbers
unchanged. Thus the complex conjugate of
, and leave real numbers
unchanged. Thus the complex conjugate of
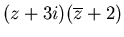 is
is
Given any true equation, you can take the complex conjugate of both sides
and get another true equation.
We can't compare complex numbers with ``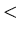 '' and ``
'' and ``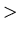 '': these only apply
to real numbers. On the other hand, ``='' does apply to complex numbers:
'': these only apply
to real numbers. On the other hand, ``='' does apply to complex numbers:
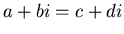 if both
if both 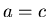 and
and 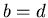 .
The absolute value of a complex number
.
The absolute value of a complex number 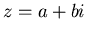 is
is
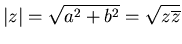 . This is the distance
in the complex plane from
. This is the distance
in the complex plane from 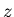 to
to 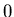 .
The roots of a quadratic equation
.
The roots of a quadratic equation
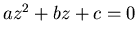 (with
(with 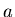 ,
,
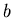 and
and 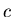 real and
real and 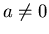 ) are
) are
If
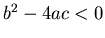 we interpret
we interpret
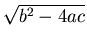 as
as
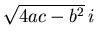 , so we have the two complex roots
, so we have the two complex roots
Note that these roots are complex conjugates of each other.
e.g. the roots of
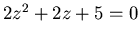 are
are
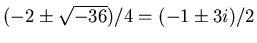 .
A much more subtle fact is that every non-constant polynomial
has roots in the complex numbers. This is the Fundamental Theorem of
Algebra.
We are also going to need to apply the exponential function to complex
numbers. The basic formulas are
.
A much more subtle fact is that every non-constant polynomial
has roots in the complex numbers. This is the Fundamental Theorem of
Algebra.
We are also going to need to apply the exponential function to complex
numbers. The basic formulas are
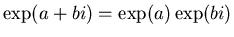 (as you might expect) and
(as you might expect) and
(which may be a surprise).
This is a definition, so it doesn't really need to be justified, but
I might note that with this definition  has its usual properties,
of which the most important for us are
has its usual properties,
of which the most important for us are
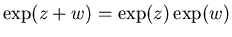 and
and
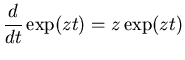 .
If
.
If 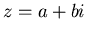 and
and 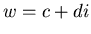 ,
,
and
Having expressed 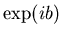 in terms of
in terms of 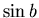 and
and 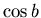 , we can
turn this around to express
, we can
turn this around to express 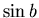 and
and 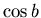 in terms of complex
exponentials:
in terms of complex
exponentials:
Note also that the trigonometric identities involving 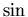 and
and 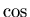 are easy to obtain from complex exponentials. For example,
are easy to obtain from complex exponentials. For example,
So
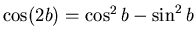 and
and
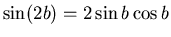 .
.
Robert Israel
2002-02-07
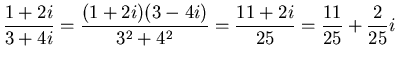 .
Complex conjugation has some important properties. To take the complex
conjugate of any algebraic expression, interchange all complex variables with
their complex conjugates, change every
.
Complex conjugation has some important properties. To take the complex
conjugate of any algebraic expression, interchange all complex variables with
their complex conjugates, change every 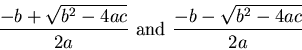
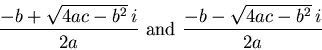
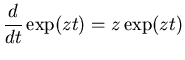 .
If
.
If