The ``Big-Oh'' notation is convenient for describing errors.
If ![]() and
and ![]() are functions defined for small positive values of
are functions defined for small positive values of ![]() ,
we write
,
we write ![]() to mean that there are positive constants
to mean that there are positive constants ![]() and
and
![]() such that
such that
Since we don't care what the constant ![]() is, we can write ``equations''
such as
is, we can write ``equations''
such as
![]() . This is shorthand for the following:
We have one function
. This is shorthand for the following:
We have one function ![]() , i.e.
, i.e.
![]() when
when ![]() is small,
and another function
is small,
and another function ![]() , i.e.
, i.e.
![]() when
when
![]() is small. Then
is small. Then
![]() , since
, since
![]() when
when ![]() is small.
is small.
Typically our ![]() will represent an error, which of course we
want to be as small
as possible. The way we could make it small is to use a small
will represent an error, which of course we
want to be as small
as possible. The way we could make it small is to use a small ![]() .
Generally, we might expect a higher order approximation to be better than a
lower order one. This is certainly true ``eventually'', i.e. for
sufficiently small values of
.
Generally, we might expect a higher order approximation to be better than a
lower order one. This is certainly true ``eventually'', i.e. for
sufficiently small values of ![]() . However, it's not necessarily true for
any particular value of
. However, it's not necessarily true for
any particular value of ![]() .
For example, if
.
For example, if ![]() and
and ![]() , then
we might expect
, then
we might expect ![]() when
when ![]() is small. But we might have,
say,
is small. But we might have,
say, ![]() and
and
![]() . It's true that
. It's true that ![]() when
when ![]() is ``small'', but in this case ``small'' means
is ``small'', but in this case ``small'' means ![]() .
.
Consider the approximation of ![]() by
by
![]() .
This has a Taylor series about
.
This has a Taylor series about
![]() (where we define
(where we define
![]() ).
The easy way to obtain the first few terms of the series is by writing
).
The easy way to obtain the first few terms of the series is by writing
![]() :
the Taylor series for
:
the Taylor series for ![]() about
about ![]() starts
starts
![]() , so
, so
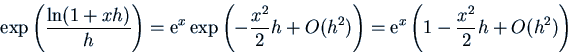
The error in the approximation is
Here is a graph showing the error ![]() as a function of
as a function of ![]() in the case
in the case
![]() , using some 34 different values of
, using some 34 different values of ![]() from
from
![]() to
to ![]() :
:
<img src="bigoh.gif">